Movimiento en un Círculo Vertical

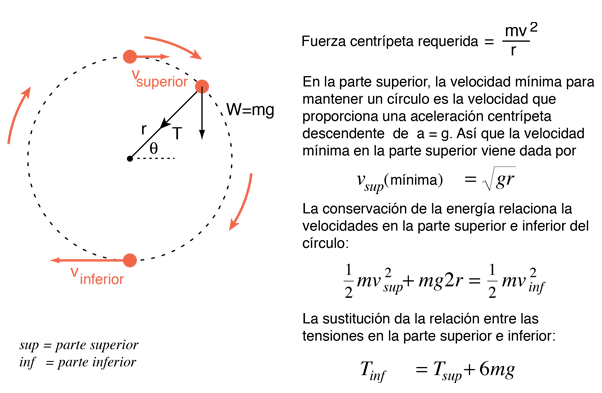
El movimiento de una masa sobre una cuerda en un círculo vertical, incluye una variedad de conceptos mecánicos. Debe satisfacer la restricción de la fuerza centrípeta para permanecer en un círculo y debe satisfacer las demandas de la conservación de la energía a medida que la energía potencial gravitacional se convierte en energía cinética cuando la masa se mueve hacia abajo. La velocidad debe incrementarse al tiempo que la masa se mueve hacia abajo desde lo alto del círculo, sujeta a las restricciones establecidas.

Para una masa moviéndose en un círculo vertical de radio r = m,

si presumimos que la cuerda permanece tensa, cuando la velocidad mínima de la masa en lo alto del círculo es (para g = 9.8 m/s2)

m/s

Esta es la condición de "ingravidez" en cualquier movimiento curvo en un plano vertical. Para cualquier velocidad por encima de este mínimo, podemos usar la conservación de la energía para relacionar la velocidad en el fondo del círculo con la velocidad en lo alto.

Para una velocidad en lo alto de vsup = m/s

la velocidad en el fondo es vfondo = m/s

Usando las condiciones de la fuerza centrífuga, la tensión en el fondo se puede relacionar con la tensión en lo alto:

Para una masa m = kg,

La tensión en lo alto del círculo es Tsup = Newtons.

La tensión correspondiente en el fondo del círculo es Tfondo = Newtons.

 Indice

Movimiento Rotacional
 
HyperPhysics*****MecánicaM Olmo R Nave
 Atrás