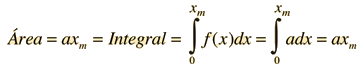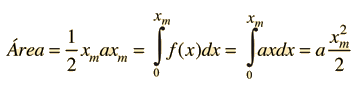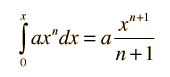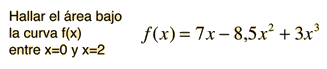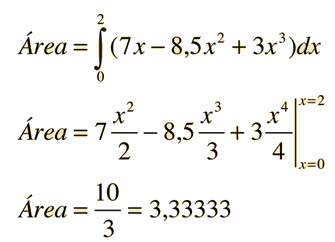Área Bajo una Curva
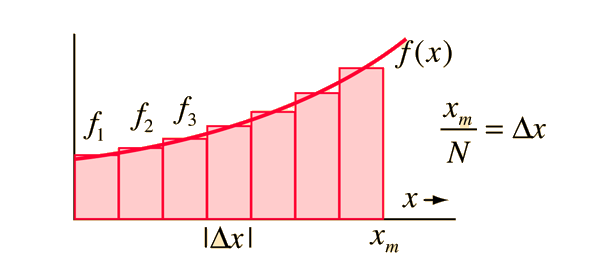
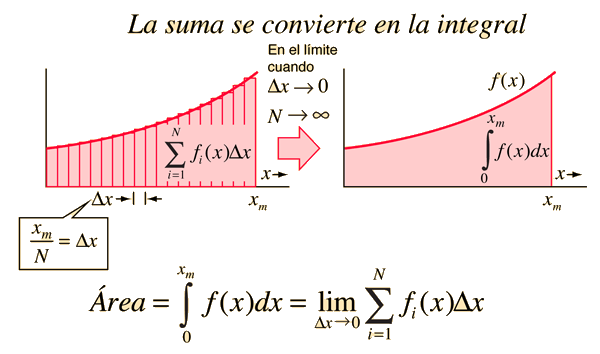
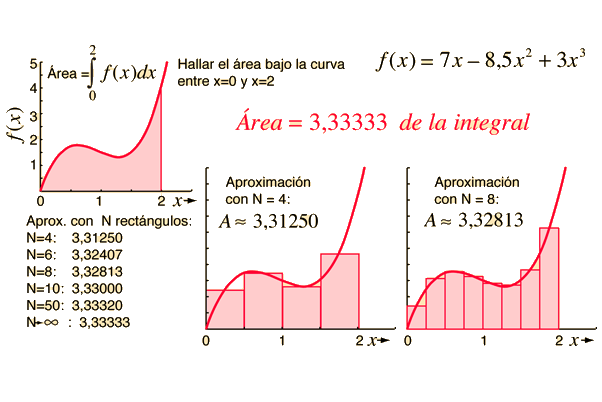
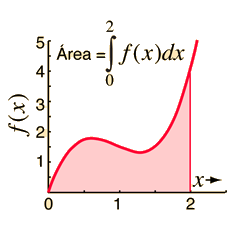
La formulación del área bajo una curva es el primer paso para desarrollar el concepto de integral. El área bajo la curva formada por el trazo de la función f(x) y el eje x se puede obtener aproximadamente, dibujando rectángulos de anchura finita y altura f igual al valor de la función en el centro del intervalo.
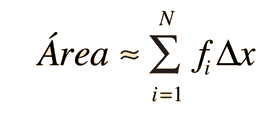
Si hacemos mas pequeño la anchura del rectángulo, entonces el número N es mas grande y mejor la aproximación al valor del área.
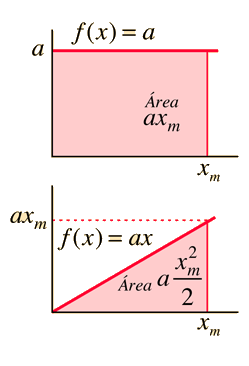
Mostrar Integrales de Áreas de Geometrías Simples.
Mostrar Aproximación del Área de una Integral.
| HyperPhysics*****HyperMath*****Cálculo | M Olmo R Nave |