Multiplicación y División
La multiplicación de números complejos en forma cartesiana es una multiplicación binomial
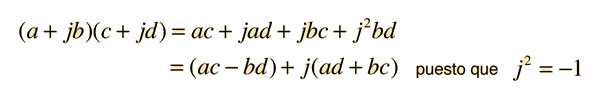
Números Complejos
| HyperPhysics****HyperMath*****Álgebra | M Olmo R Nave |
Multiplicación y DivisiónLa multiplicación de números complejos en forma cartesiana es una multiplicación binomial 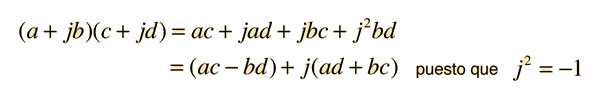 |
Índice Números Complejos | ||
|
Atrás |
Racionalización de Números ComplejosLa división de números complejos que se expresan en forma cartesiana se facilita por un proceso llamado racionalización. La forma de fracción 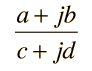 presenta dificultades, debido a la parte imaginaria del denominador. El denominador se puede forzar a ser real, multiplicando ambos numerador y denominador por el conjugado del denominador. 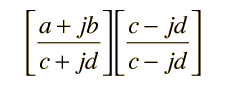 Expandiéndolo, se pone de nuevo el resultado de la división en forma cartesiana. 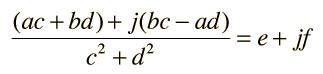 Cálculo de la Multiplicación y la División |
Índice Números Complejos | ||
|
Atrás |
Conjugado ComplejoEl conjugado de un número complejo es ese mismo número, pero con el signo de la parte imaginaria invertido 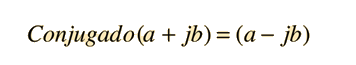 La utilidad que tiene el conjugado es que, cualquier número complejo multiplicado por su conjugado es un número real: 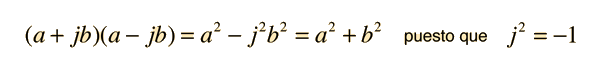 Esta operación tiene utilidad práctica en la racionalización de números complejos. La raiz cuadrada de un número complejo multiplicado por su conjugado es la magnitud del número complejo cuando se expresa en forma polar. Aplicaciones |
Índice Números Complejos | ||
|
Atrás |
Aplicaciones de Conjugados ComplejosCuando se necesita una definida cantidad positiva real de una función real, se puede usar el cuadrado de la función. En el caso de una función compleja, se usa el conjugado complejo para acometer este propósito. El producto de un número complejo y su conjugado complejo es el número complejo análogo a elevar al cuadrado una función real. El conjugado complejo se usa en la racionalización de números complejos y para obtener la amplitud de la forma polar del número complejo. Una aplicación en Física del conjugado complejo la tenemos en el cálculo de la probabilidad en mecánica cuántica. Puesto que la función de onda que define la amplitud puede ser una función compleja, se define la probabilidad en términos del conjugado complejo para obtener un valor real. 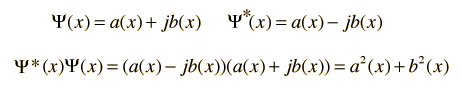 |
Índice Números Complejos | ||
|
Atrás |