Fuerza de gravedad dentro de una esfera hueca
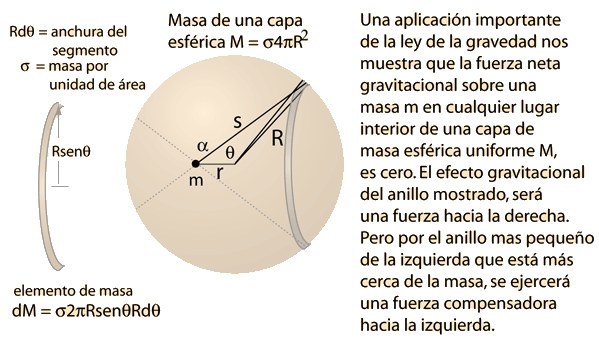
Para la aplicación de la ley de la gravedad dentro de una esfera hueca uniforme de masa M, se elige un punto sobre el eje de una tira circular de masa. El problema se plantea, dividiendo en capas delgadas infinitesimalmente la superficie de la esfera de densidad σ por unidad de área. Se obtiene así anillos circulares de anchura infinitesimal. La elección de tal punto no conlleva ninguna pérdida de generalidad, porque para cualquier punto dentro de la esfera, los elementos de masa se pueden elegir, tal que el punto esté sobre el eje de simetría.
Para establecer la integral necesaria, se usa el triángulo de arriba, donde aprovechamos la simetría del sistema. Todas las componentes de la fuerza de la gravedad perpendicular a r, se cancelarán por simetría, y todas las componentes a lo largo de r, sumarán. El elemento de fuerza diferencial sobre la masa m se puede escribir
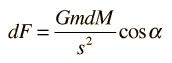
donde el elemento diferencial de masa dM es dado por
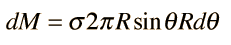
La fuerza ejercida por la entera esfera hueca se puede expresar como una integral sobre el ángulo θ
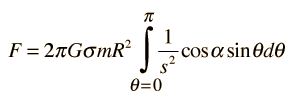
Para evaluar la integral, las variables s y α se deben expresar en términos del ángulo θ . Usando la Ley de los cosenos con el ángulo interior θ da
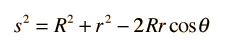
y esto se puede diferenciar para dar
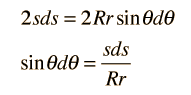
Ahora, usando la ley de los cosenos para el ángulo externo α:
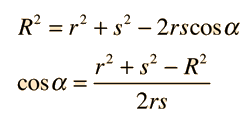
Con estas relaciones, podemos expresar la integral en términos de s en vez de θ. Hasta este punto, el tratamiento ha sido igual que el empleado para un punto fuera de la esfera, pero ahora la forma de los límites son diferentes. Para θ = 0, s = R - r, y para θ = π, s = r + R .
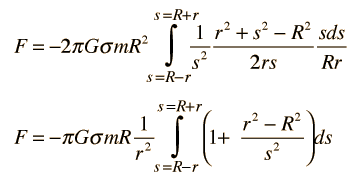
Usando la expresión de densidad de área σ = M/4πR2, the integral can be written
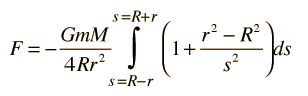
Ahora, las partes se evaluan como integrales polinómicas y simplificado.
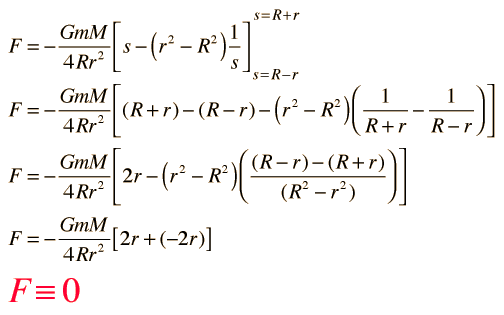
¡La fuerza de gravedad neta ejercida sobre una masa puntual, situada en el interior de una masa esférica hueca es exactamente cero! Físicamente esto supone un resultado muy importante porque cualquier distribución de masa esférica y simétrica, fuera de la posición de la masa de prueba m, se puede construir como una serie de tales esferas. Esto prueba que la fuerza de gravedad de cualquier distribución de masa esférica y simétrica dentro de su radio es cero. Si una masa dada m está en el interior de un distribución de masa esférica y simétrica, la parte de la masa fuera de su radio no contribuye con ninguna fuerza neta.
| Fuerza de gravedad sobre una masa situada fuera de una esfera hueca |
| Ejemplo de caída a través del centro de la Tierra |
Leyes de Newton
Conceptos sobre gravedad
| HyperPhysics***** Mecánica | M Olmo | R Nave |