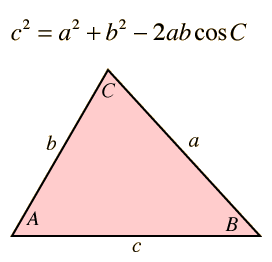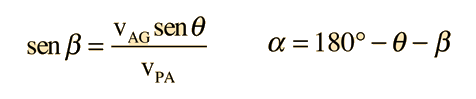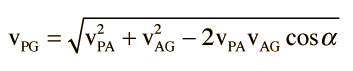| Haga clic en el texto seleccionado, ya sea para el lado c o el ángulo C, o para iniciar el cálculo. |
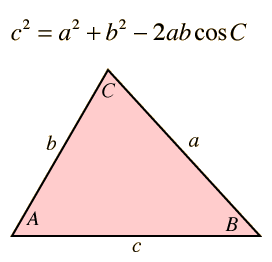 |
Entrar datos para los lados a y b y uno de lado c, o ángulo C. Luego haga clic en el texto activo de la cantidad desconocida que desea calcular.
El cálculo del lado c es directo, pero el cálculo de los lados a o b es más complicado, puesto que cambiando cualquiera de c o ángulo C, fuerza el cambio en ambos lados a y b. Para calcular a o b, primero use la ley de los senos para encontrar el ángulo opuesto al lado que desee calcular. A continuación, utilice la ley de los cosenos para encontrar la longitud del lado desconocido.
|