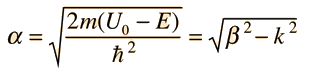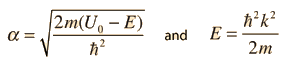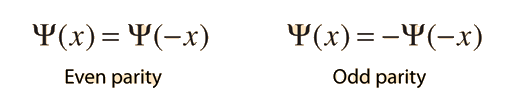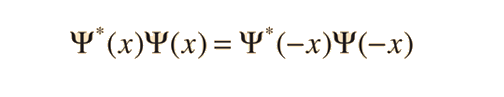Particle in Finite-Walled Box
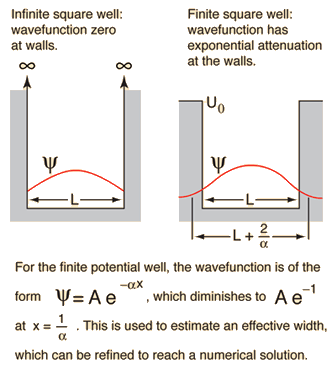
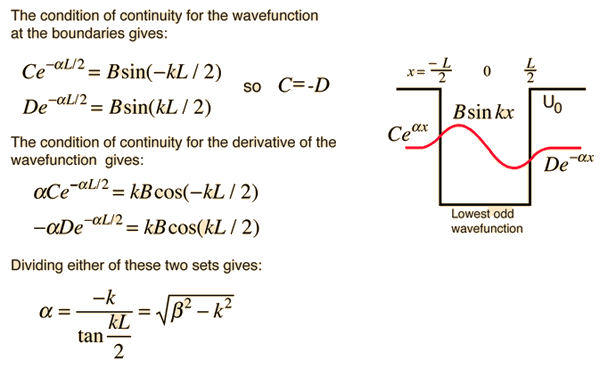
Given a potential well as shown and a particle of energy less than the height of the well, the solutions may be of either odd or even parity with respect to the center of the well. The Schrodinger equation gives trancendental forms for both, so that numerical solution methods must be used.
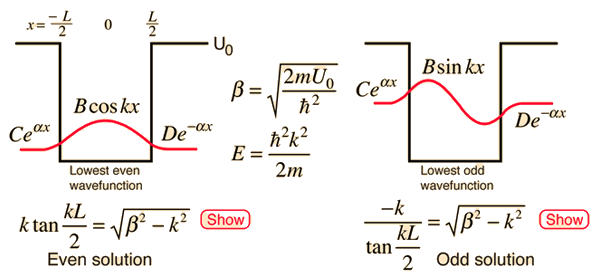
Schrodinger equation concepts
| HyperPhysics***** Quantum Physics | R Nave |