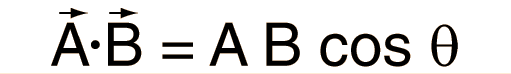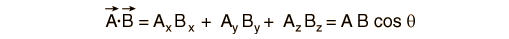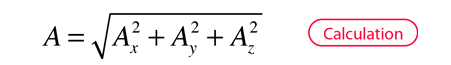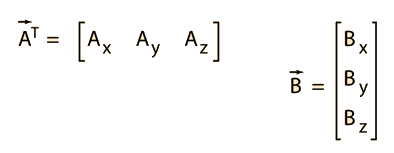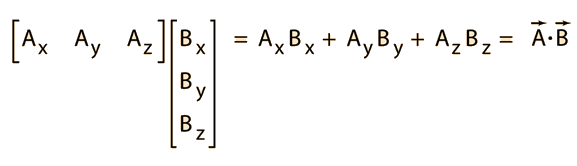Scalar Product of Vectors

The scalar product and the vector product are the two ways of multiplying vectors which see the most application in physics and astronomy. The scalar product of two vectors can be constructed by taking the component of one vector in the direction of the other and multiplying it times the magnitude of the other vector. This can be expressed in the form:

If the vectors are expressed in terms of unit vectors i, j, and k along the x, y, and z directions, the scalar product can also be expressed in the form:

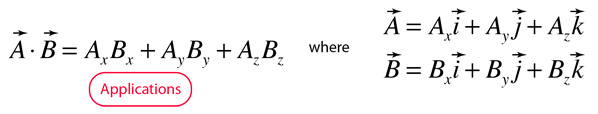
The scalar product is also called the "inner product" or the "dot product" in some mathematics texts.

Scalar Product Calculation

You may enter values in any of the boxes below. Then click on the symbol for either the scalar product or the angle. The vectors A and B cannot be unambiguously calculated from the scalar product and the angle. If the angle is changed, then B will be placed along the x-axis and A in the xy plane.

The scalar product = ( )( )(cos ) degrees.

()()+()()+()() =

Note: The numbers above will not be forced to be consistent until you click on either the scalar product or the angle in the active formula above.

Scalar Product Applications

Geometrically, the scalar product is useful for finding the direction between arbitrary vectors in space. Since the two expressions for the product:

involve the components of the two vectors and since the magnitudes A and B can be calculated from the components using:

then the cosine of the angle can be calculated and the angle determined.

One important physical application of the scalar product is the calculation of work:

The scalar product is used for the expression of magnetic potential energy and the potential of an electric dipole.

Matrix Representation of Scalar Product

It is sometimes convenient to represent vectors as row or column matrices, rather than in terms of unit vectors as was done in the scalar product treatment above. If we treat ordinary spatial vectors as column matrices of their x, y and z components, then the transposes of these vectors would be row matrices. We could then write for vectors A and B:

Then the matrix product of these two matrices would give just a single number, which is the sum of the products of the corresponding spatial components of the two vectors. This number is then the scalar product of the two vectors.

When represented this way, the scalar product of two vectors illustrates the process which is used in matrix multiplication, where the sum of the products of the elements of a row and column give a single number.