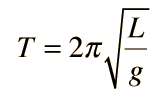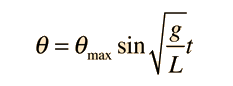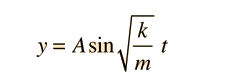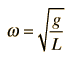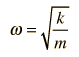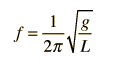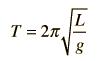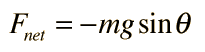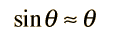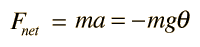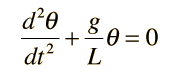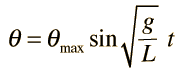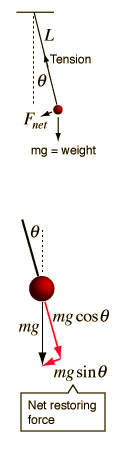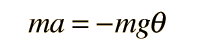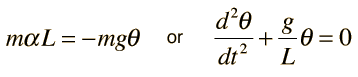Simple Pendulum
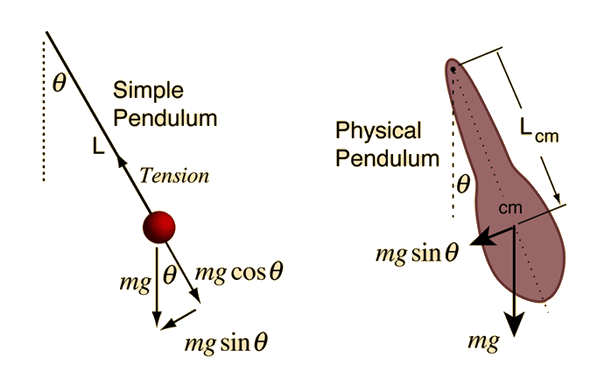
A simple pendulum is one which can be considered to be a point mass suspended from a string or rod of negligible mass. It is a resonant system with a single resonant frequency. For small amplitudes, the period of such a pendulum can be approximated by:
Note that the angular amplitude does not appear in the expression for the period. This expression for period is reasonably accurate for angles of a few degrees, but the treatment of the large amplitude pendulum is much more complex. | 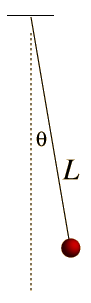 |
If the rod is not of negligible mass, then it must be treated as a physical pendulum. |
Sean Carroll relates the story of Galileo's discovery of the fact that for small amplitudes, the period and frequency are unaffected by the amplitude. "In 1581, a young Galileo Galilei reportedly made a breakthrough discovery while he sat bored during a church service in Pisa. The chandelier overhead would swing gently back and forth, but it seemed to move more quickly when it was swinging widely (after a gust of wind, for example) and more slowly when it wasn't moving as far. Intrigued, Galileo decided to measure how much time it took for each swing, using the only approximately periodic event to which he had ready access: the beating of his own pulse. He found something interesting: The number of heartbeats between swings of the chandelier was roughly the same, regardless of whether the swings were wide or narrow. The size of the oscillations - how far the pendulum swung back and forth - didn't affect the frequency of those oscillations."
Periodic motion concepts
Carroll
Eternity to Here, p16
| HyperPhysics***** Mechanics | R Nave |