Physical Pendulum
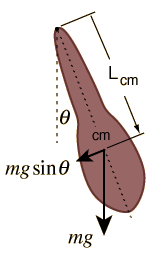 |
Hanging objects may be made to oscillate in a manner similar to a simple pendulum. The motion can be described by "Newton's 2nd law for rotation": 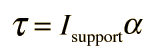 where the torque is 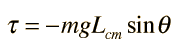 and the relevant moment of inertia is that about the point of suspension. The resulting equation of motion is: 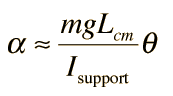 |
| for small angles where | 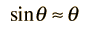 |
|
This is identical in form to the equation for the simple pendulum and yields a period:
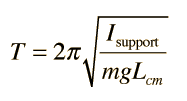
| Calculation | Compare to simple pendulum |
| Rod pendulum | Circular geometries | Combinations |
Periodic motion concepts
| HyperPhysics***** Mechanics | R Nave |