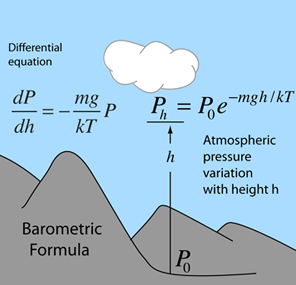
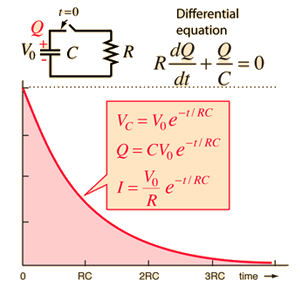
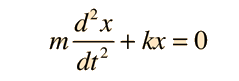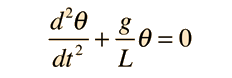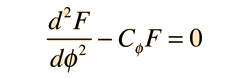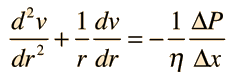Second Order Homogeneous DE
A linear second order homogeneous differential equation involves terms up to the second derivative of a function. For the case of constant multipliers, The equation is of the form
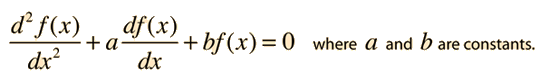
and can be solved by the substitution

The solution which fits a specific physical situation is obtained by substituting the solution into the equation and evaluating the various constants by forcing the solution to fit the physical boundary conditions of the problem at hand. Substituting gives
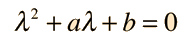
which leads to a variety of solutions, depending on the values of a and b. In physical problems, the boundary conditions determine the values of a and b, and the solution to the quadratic equation for λ reveals the nature of the solution.
Case I: Two real roots
For values of a and b such that
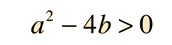
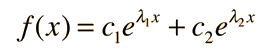
Case II: A real double root
If a and b are such that
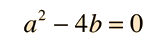
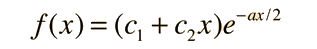
Case III: Complex conjugate roots
For values of a and b such that
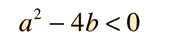

The solution to the homogeneous equation is important on its own for many physical applications, and is also a part of the solution of the non-homogeneous equation.
Applications
References
Kreyzig
Ch 2
| HyperPhysics****HyperMath*****Differential equations | R Nave |