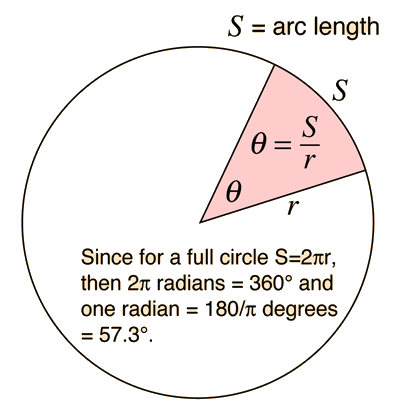
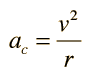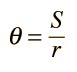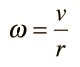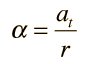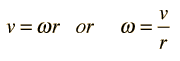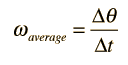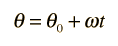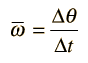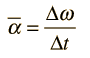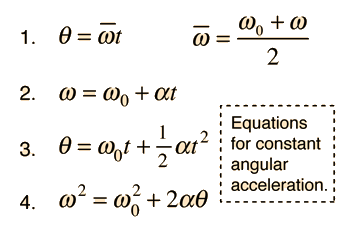Comments on Rotation Calculation
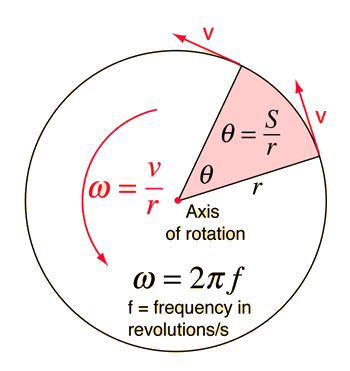
In the example calculation in the section Rotation Equations above, some assumptions were made about the calculation order. The rotation equations represent a complete set of equations for constant angular acceleration rotations, but in certain types of problems, intermediate results must be calculated before proceeding to the final calculation. In the example calculation, you may have to do intermediate calculations, e.g., to establish the final angular velocity, in order to set up the problem you wish to solve, just as if you were working the problem with calculator and paper.
In the example calculation, the time, initial angular velocity, and angular displacement were considered given (primary) unless they were being calculated (e.g., in calculating α). If θ is being calculated, then ω is assumed given, so it must be calculated first if you want to specify α. If initial angular velocity is being calculated, then ω is presumed given. If time is being calculated then α is presumed given. These presumptions are included in the Javascript routines.
|
Index |