Bose-Einstein Condensation
In 1924 Einstein pointed out that bosons could "condense" in unlimited numbers into a single ground state since they are governed by Bose-Einstein statistics and not constrained by the Pauli exclusion principle. Little notice was taken of this curious possibility until the anomalous behavior of liquid helium at low temperatures was studied carefully.
When helium is cooled to a critical temperature of 2.17 K, a remarkable discontinuity in heat capacity occurs, the liquid density drops, and a fraction of the liquid becomes a zero viscosity "superfluid". Superfluidity arises from the fraction of helium atoms which has condensed to the lowest possible energy.
A condensation effect is also credited with producing superconductivity. In the BCS Theory, pairs of electrons are coupled by lattice interactions, and the pairs (called Cooper pairs) act like bosons and can condense into a state of zero electrical resistance.
The conditions for achieving a Bose-Einstein condensate are quite extreme. The participating particles must be considered to be identical, and this is a condition that is difficult to achieve for whole atoms. The condition of indistinguishability requires that the deBroglie wavelengths of the particles overlap significantly. This requires extremely low temperatures so that the deBroglie wavelengths will be long, but also requires a fairly high particle density to narrow the gap between the particles.
Since the 1990s there has been a surge of research into Bose-Einstein condensation since it was discovered that Bose-Einstein condensates could be formed with ultra-cold atoms. The use of laser cooling and the trapping of ultra-cold atoms with magnetic traps has produced temperatures in the nanokelvin range. Cornell and Wieman along with Ketterle of MIT received the 2001 Nobel Prize in Physics "for the achievement of Bose-Einstein condensation in dilute gases of alkali atoms, and for early fundamental studies of the properties of the condensates". Cornell and Wieman led an active group at the University of Colorado, Boulder which has produced Bose-Einstein condensates with rubidium atoms. Other groups at MIT, Harvard and Rice have been very active in this rapidly advancing field. | 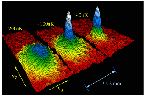 |
| HyperPhysics***** Quantum Physics ***** Particles | R Nave |