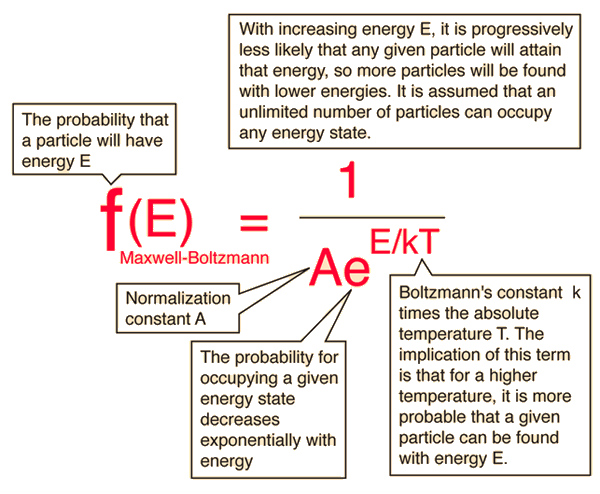
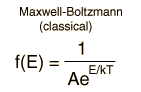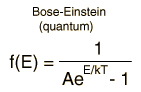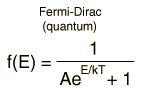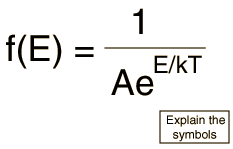The Maxwell-Boltzmann Distribution
The Maxwell-Boltzmann distribution is the classical distribution function for distribution of an amount of energy between identical but distinguishable particles.
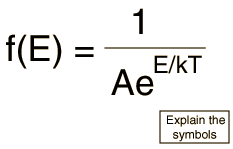
Besides the presumption of distinguishability, classical statistical physics postulates further that:
- There is no restriction on the number of particles which can occupy a given state.
- At thermal equilibrium, the distribution of particles among the available energy states will take the most probable distribution consistent with the total available energy and total number of particles.
- Every specific state of the system has equal probability.
One of the general ideas contained in these postulates is that it is unlikely that any one particle will get an energy far above the average (i.e., far more than its share). Energies lower than the average are favored because there are more ways to get them. If one particle gets an energy of 10 times the average, for example, then it reduces the number of possibilities for the distribution of the remainder of the energy. Therefore it is unlikely because the probability of occupying a given state is proportional to the number of ways it can be obtained.
|
Index
Applied statistics concepts
Reference
Blatt
Ch. 11. |