Scattering Cross Section
The concept of cross section, as its name suggests, is that of effective area for collision. The cross section of a spherical target is
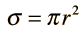 |
|
In aiming a beam of particles at a target which is much smaller than the beam, as in the Rutherford scattering experiment, the cross section takes on a statistical nature.
Rutherford worked out the scattering cross section for alpha particles of kinetic energy KE scattering off a single nucleus with atomic number Z. The cross section for scattering at a greater angle than some chosen angle is
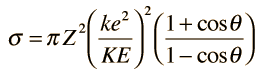 |
|
More detail is needed for the prediction of the number of scattering events to expect above that angle. When the details about the beam and target are included, the fractional scattering rate is given by

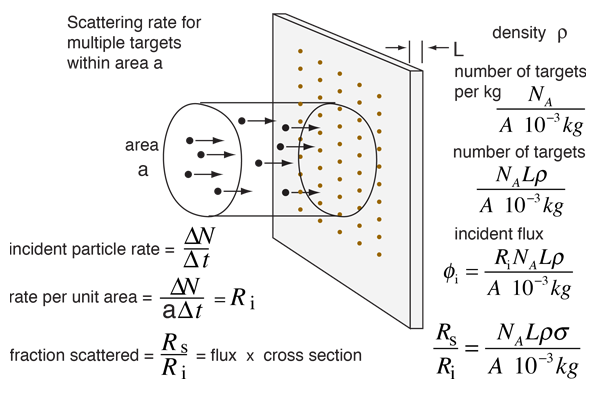
This calculation is designed for the calculation of cross section and scattered fraction only. Note that the standard assumptions of Rutherford scattering apply, so that the calculation works only for film thicknesses of a few micrometers or less. Default values will be entered for unspecified parameters, but all values except the cross section and scattered fraction can be changed.
| Numerical example: gold foil |
Rutherford concepts
| HyperPhysics***** Nuclear | R Nave |
