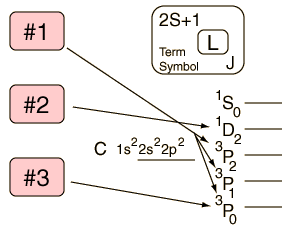
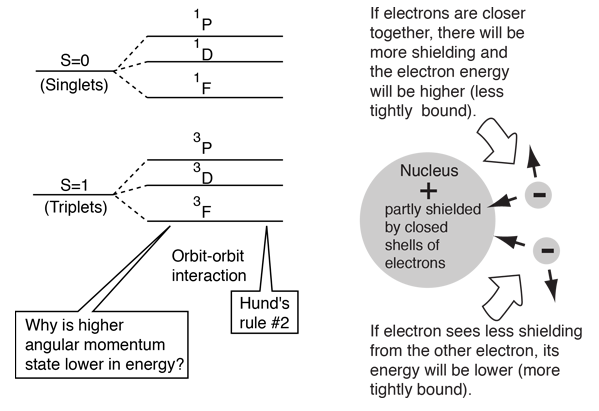
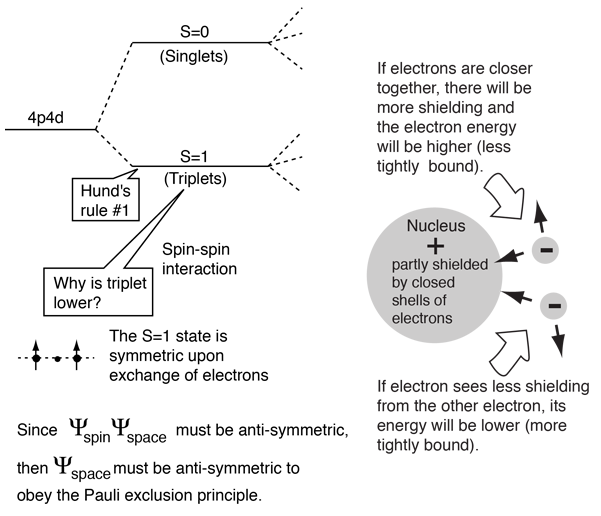
Hund's Rules

1. The term with maximum multiplicity lies lowest in energy.	Click on the indicated buttons for more detail.
2. For a given multiplicity, the term with the largest value of L lies lowest in energy.
3. For atoms with less than half-filled shells, the level with the lowest value of J lies lowest in energy.
Hund's rules assume combination to form S and L, or imply L-S (Russell-Saunders) coupling.

Note: Some references, such as Haken & Wolf, use Hund's Rule #1 to apply to the nature of full shells and subshells. Full shells and subshells contribute nothing to the total angular momenta L and S. If you call this Hund'e Rule #1, then the above rules will be bumped up one in number. I don't know which is the more common practice.

Hund's Rule #1

The term with the maximum multiplicity lies lowest in energy.

The explanation of the rule lies in the effects of the spin-spin interaction. Though often called by the name spin-spin interaction, the origin of the energy difference is in the coulomb repulsion of the electrons. It's just that a symmetric spin state forces an antisymmetric spatial state where the electrons are on average further apart and provide less shielding for each other, yielding a lower energy. The sketches below attempt to visualize why that is so.

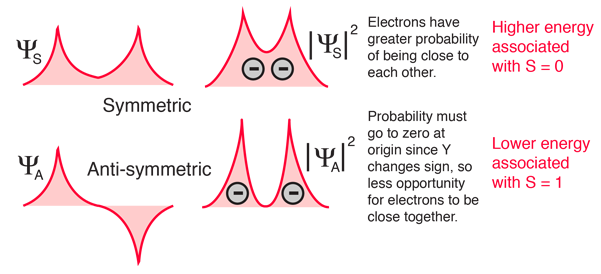
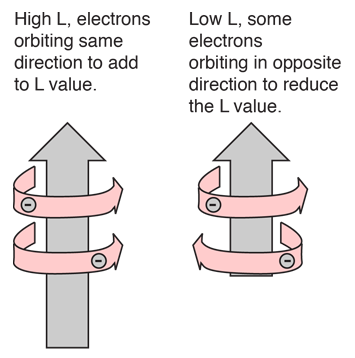
These sketches are conceptual only. No attempt has been made to do any realistic scaling.

Note that the energies we are discussing here are electric potential energies, so that a negative electron in the vicinity of a positive nucleus will have a negative energy leading to a bound state. Any force between the electrons will tend to counter that, contributing a positive potential energy which makes the electrons less tightly bound, or higher in potential energy.

Hund's Rule #2

For a given multiplicity, the term with the largest value of L lies lowest in energy.

Example: In the configuration p² we expect the order ³P < ¹D < ¹S).

The basis for this rule is essentially that if the electrons are orbiting in the same direction (and so have a large total angular momentum) they meet less often than when they orbit in opposite directions. Hence their repulsion is less on average when L is large.

These influences on the atomic electron energy levels is sometimes called the orbit-orbit interaction. The origin of the energy difference lies with differences in the coulomb repulsive energies between the electrons.

For large L value, some or all of the electrons are orbiting in the same direction. That implies that they can stay a larger distance apart on the average since they could conceivably always be on the opposite side of the nucleus. For low L value, some electrons must orbit in the opposite direction and therefore pass close to each other once per orbit, leading to a smaller average separation of electrons and therefore a higher energy.

Hund's Rule #3

For atoms with less than half-filled shells, the level with the lowest value of J lies lowest in energy.

Example: Since p² is less than half-filled, the three levels of ³P are expected to lie in the order ³P₀ < ³P₁ < ³P₂ .

When the shell is more than half full, the opposite rule holds (highest J lies lowest). The basis for the rule is the spin-orbit coupling. The scalar product S·L is negative if the spin and orbital angular momentum are in opposite directions. Since the coefficient of S·L is positive, lower J is lower in energy.

Exceptions to Hund's Rules

Hund's rules presume L-S coupling and presume that the electrons can be considered to be in a unique configuration. Neither is always true. For heavier elements, the "j-j coupling" scheme often gives better agreement with experiment.