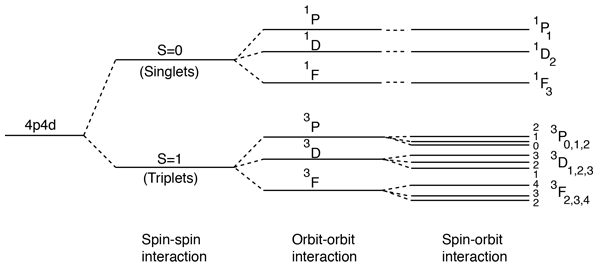
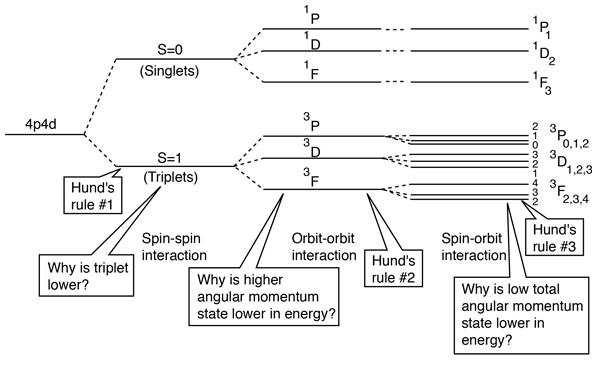
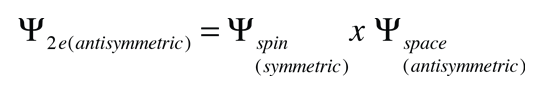Spin-Spin Interaction
The effect of the spin-spin interaction is noted in Hund's rule #1. If you have two electrons, then the state in which their spins are parallel (S=1, triplet state) will be lower in energy than the state in which their spins are antiparallel (S=0, singlet state).
This result is correlated with the fact that the two electrons are identical fermions, and a wavefunction which describes the pair must be antisymmetric with respect to exchange of the electrons ( a requirement of the Pauli exclusion principle). The wavefunction can be considered to be the product of the space and spin wavefunctions:
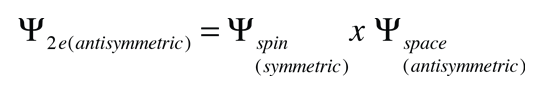
The fact that the spins are parallel makes the spin part of the wavefunction symmetric, and forces the space part to be antisymmetric. An anti-symmetric space wavefunction for the two electrons implies a larger average distance between them than a symmetric function of the same type. The probability is the square of the wavefunction, and from a simple functional point of view, the square of an antisymmetric function must go to zero at the origin. So in general, the probability for small separations of the two electrons is smaller than for a symmetric space wavefunction. If the electrons are on the average further apart, then there will be less shielding from the nucleus by the other electron, and a given electron will therefore be more exposed to the nucleus. This implies that it will be more tightly bound and of lower energy.
|
Index
Atomic structure concepts |