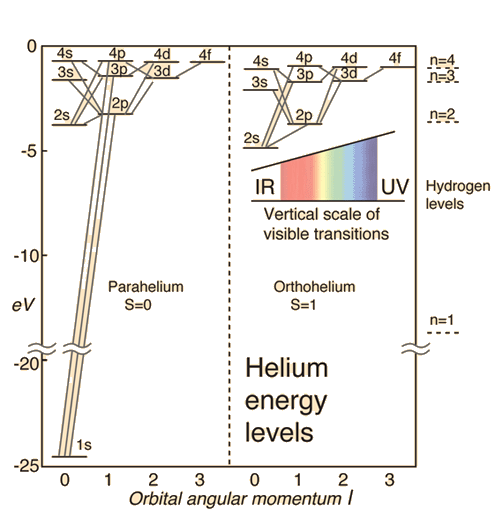
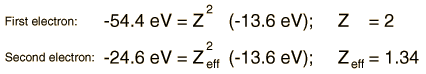Orthohelium and Parahelium Energy Levels
In the helium energy level diagram, one electron is presumed to be in the ground state of a helium atom, the 1s state. An electron in an upper state can have spin antiparallel to the ground state electron (S=0, singlet state, parahelium) or parallel to the ground state electron (S=1, triplet state, orthohelium).
It is observed that the orthohelium states are lower in energy than the parahelium states. The explanation for this is:
- The parallel spins make the spin part of the wavefunction symmetric.
- The total wavefunction for the electrons must be anti-symmetric since they are fermions and must obey the Pauli exclusion principle.
- This forces the space part of the wavefunction to be anti-symmetric. The wavefunction for the electrons can be written as the product of the space and spin parts of the wavefunction.
- An anti-symmetric space wavefunction for the two electrons implies a larger average distance between them than a symmetric function of the same type. The probability is the square of the wavefunction, and from a simple functional point of view, the square of an antisymmetric function must go to zero at the origin. So in general, the probability for small separations of the two electrons is smaller than for a symmetric space wavefunction.
- If the electrons are on the average further apart, then there will be less shielding of the nucleus by the ground state electron, and the excited state electron will therefore be more exposed to the nucleus. This implies that it will be more tightly bound and of lower energy.
This effect is sometimes called the "spin-spin interaction" and is addressed by Hund's Rule #1 . It is part of the understanding of the ordering of energy levels in multi-electron atoms.
|
Index
Reference
Rohlf
Ch 9 |