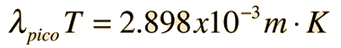Temperaturas de Estrellas
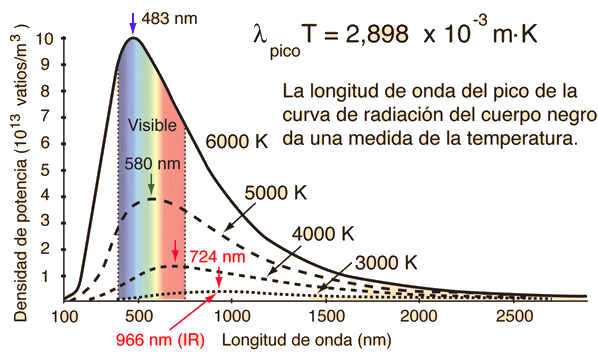
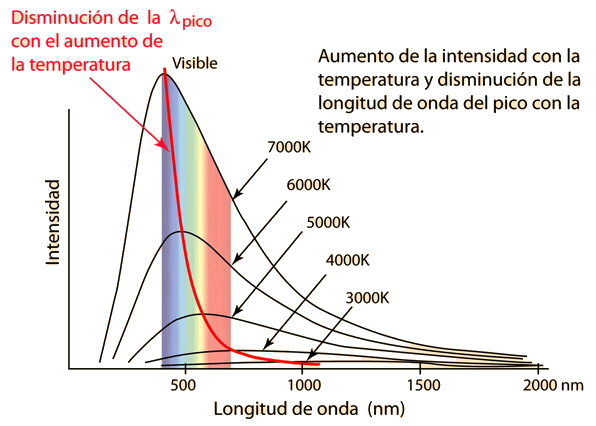
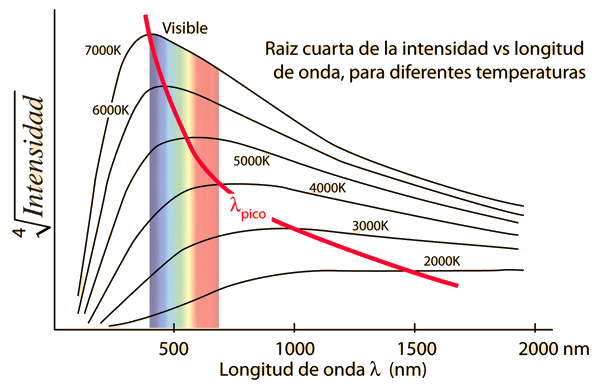
Las estrellas se aproximan a radiadores de cuerpo negro, y sus colores visibles dependen de la temperatura del radiador. Las curvas muestran estrellas azules, blancas y rojas. La estrella blanca se ajusta a 5270K, de modo que el pico de su curva de cuerpo negro, está a la longitud de onda de pico del Sol, 550 nm. La temperatura se puede deducir de la longitud de onda del pico, por medio de la ley de desplazamiento de Wien.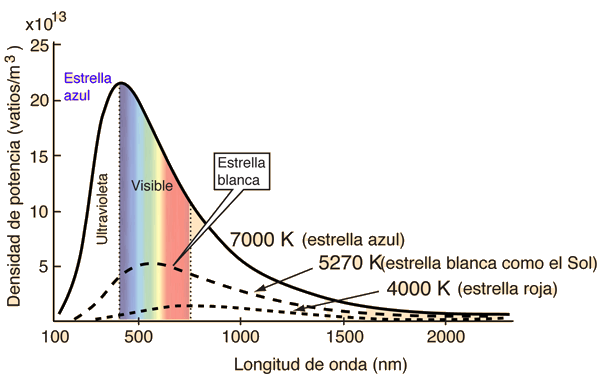
El cambio en el color visual de estrellas de diferentes temperaturas, puede ser trazado sobre un diagrama de cromaticidad.
Clasificación de Estrellas
Conceptos de Radiación de Cuerpo Negro
| HyperPhysics*****Física Cuántica | M Olmo R Nave |