Entropía y el Ciclo de Carnot
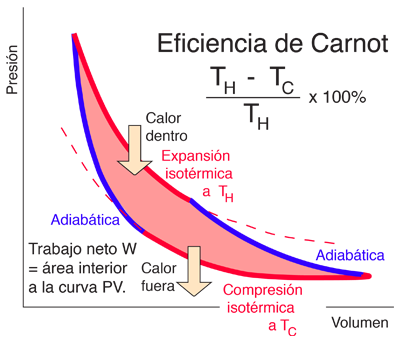 |
La eficiencia de un ciclo de motor térmico, está dado por 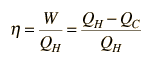 Para el caso ideal del ciclo de Carnot, esta eficiencia se puede escribir 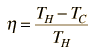 |
Usando juntas estas dos expresiones
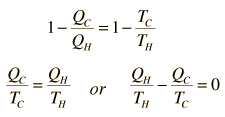
Si tomamos Q para representar el calor añadido al sistema, entonces el calor tomado del sistema tendrá un valor negativo. Para el ciclo de Carnot
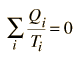
que se puede generalizar como una integral alrededor de un ciclo reversible
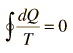 | Teorema de Clausius |
Para cualquier parte del ciclo de motor térmico, se puede usar esto para definir el cambio en la entropía S del sistema
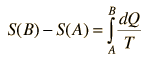
o en forma diferencial en cualquier punto del ciclo
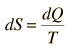
Para cualquier proceso irreversible, la eficiencia es menor que la del ciclo de Carnot. Esto se puede asociar con un menor flujo de calor hacia el sistema y/o mas flujo de calor hacia fuera del sistema. El resultado inevitable es
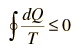 | Desigualdad de Clausius |
Cualquier ciclo de motor real se traducirá en más entropía entregada al medio ambiente que tomada de él, dando lugar a un aumento neto total de la entropía.
| Mayor Detalle sobre la Desigualdad de Clausius |
Conceptos sobre el Ciclo de Carnot
Conceptos sobre Motores Térmicos
Conceptos sobre Entropía/a>
| HyperPhysics*****Termodinámica | M Olmo R Nave |