Potencia Radiada por un Cuerpo Negro
Cuando aumenta la temperatura de un radiador de cuerpo negro, la energía radiada total aumenta, y el pico de la curva de radiación se mueve hacia longitudes de onda más cortas. Cuando se evalúa el máximo a partir de la fórmula de radiación de Planck, se encuentra que el producto de la longitud de onda máxima por la temperatura, es una constante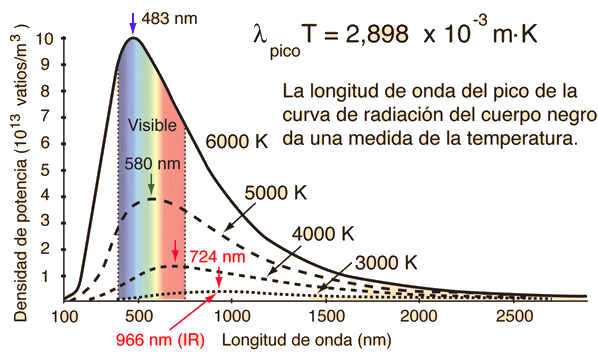
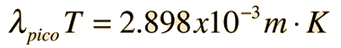 |
|
La potencia radiada en un determinado intervalo de longitud de onda Δλ a la longitud de onda λ se puede aproximar por
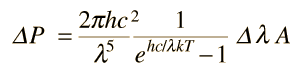
El cálculo aproximado de arriba de la potencia radiada en un rango de longitud de onda elegido, es una suma de fuerza bruta de más de 100 términos, formados dividiendo el rango de longitud de onda especificado en 100 partes. Esto se compara luego con la potencia radiada total, calculada a partir de la ecuación de Stefan-Boltzmann. Se puede comprobar el cálculo, seleccionando el rango de longitud de onda, para que cubra esencialmente toda la energía radiada. Se encontrará que el cálculo difiere si se tiene que elegir una longitud de onda de partida muy cercana a cero, y si se pone una longitud de onda demasiado grande. Sin embargo, al examinar la gama de longitud de onda para la cual la potencia radiada parece ser significativa, se pueden elegir límites razonables de la longitud de onda, y confirmar que se obtiene esencialmente toda la potencia radiada.
Conceptos de Radiación de Cuerpo Negro
| HyperPhysics*****Física Cuántica | M Olmo R Nave |