El Efecto Lamb
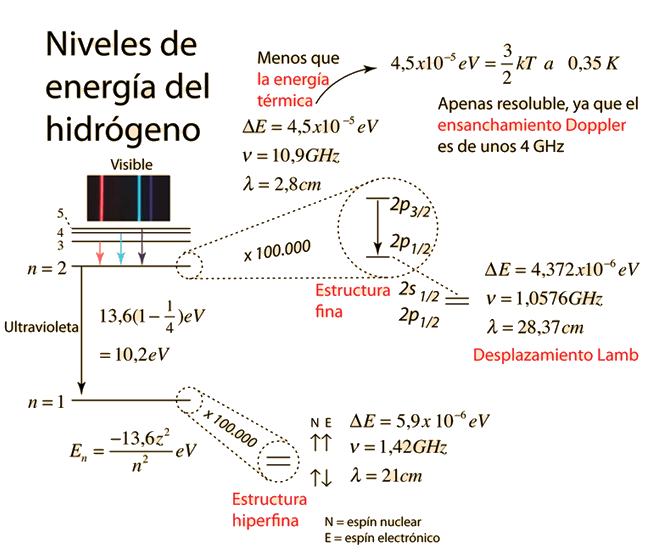
De acuerdo con la solución de la ecuación de Schrodinger para el hidrógeno, los niveles de energía del electrón del hidrógeno debería depender solamente del número cuántico principal n. En 1951, Willis Lamb descubrió que no era así -que el estado 2p(1/2), era ligeramente inferior al estado 2s(1/2), resultando en un ligero desplazamiento de la línea espectral correspondiente (el efecto Lamb)-.
Podría parecer que un efecto tan pequeño, se consideraría insignificante, pero en este caso ese desplazamiento sondeó las profundidades de nuestra comprensión de la teoría electromagnética. | 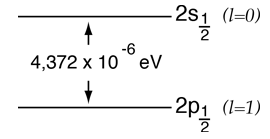 |
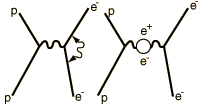 | En el corazón del proceso está la fuerza de intercambio, por la cual, las cargas interactuan mediante el intercambio de fotones (el modelo de fuerza de intercambio de la fuerza electromagnética). Puede haber una interacción propia del electrón, por intercambio de un fotón como se ilustra en el diagrama de Feynman a la izquierda. Esto "borra" la posición del electrón en un intervalo de aproximadamente 0,1 fermi (radio de Bohr = 52.900 fermis). Esto hace que el factor g del espín del electrón, sea ligeramente diferente de 2. También hay un ligero debilitamiento de la fuerza sobre el electrón, cuando está muy próximo al núcleo, haciendo que el electrón 2s (que tiene una penetración total hasta el núcleo), sea ligeramente más alto en energía que el electrón 2p(1/2). |
Cuando decimos que la penetración del electrón 2s más cerca del núcleo, conduce a una energía mayor que la del 2p, parece directamente contradictorio con la situación de átomos con múltiples electrones. Allí, la penetración del electrón 2s más cerca del núcleo, significa que ha penetrado en el interior del electrón 1s, y por lo tanto siente una atracción mas fuerte hacia el núcleo positivo, lo que lleva a un nivel de energía inferior (se necesita más energía para eliminar del átomo el electrón 2s, que el 2p). Pero en el caso del átomo de hidrógeno, sólo hay un electrón, por lo que cuando están en los estados excitados 2s ó 2p, no hay ningún blindaje de electrones internos. El efecto sobre los niveles de energía tiene un origen completamente diferente, modelado por la electrodinámica cuántica. En ausencia de este efecto, los electrones 2s y 2p tendrían energías idénticas, ya que no hay blindaje por la presencia de otros electrones. La "auto-interacción" del electrón cuando está cerca del protón, origina el efecto de "borrado" de la carga del electrón, de manera que su atracción hacia el protón, es un poco más débil de lo que debería haber sido. Esto significa que ha encontrado una interacción, que lo hace ligeramente menos unido que un electrón 2p, por lo tanto, con mayor energía.
Active illustration: click for more detail
| Medición de Microondas del Efecto Lamb | Significado del Efecto Lamb |
| Medición del Efecto Lamb por Espectroscopia de Saturación |
Conceptos de la Ecuación de Schrödinger
Conceptos del Hidrógeno
Referencia
Rohlf
Sec 8-9.
| HyperPhysics*****Física Cuántica | M Olmo R Nave |
