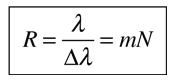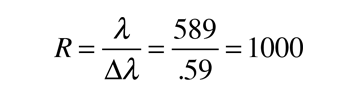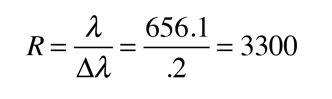Resolvancia de Red de Difracción
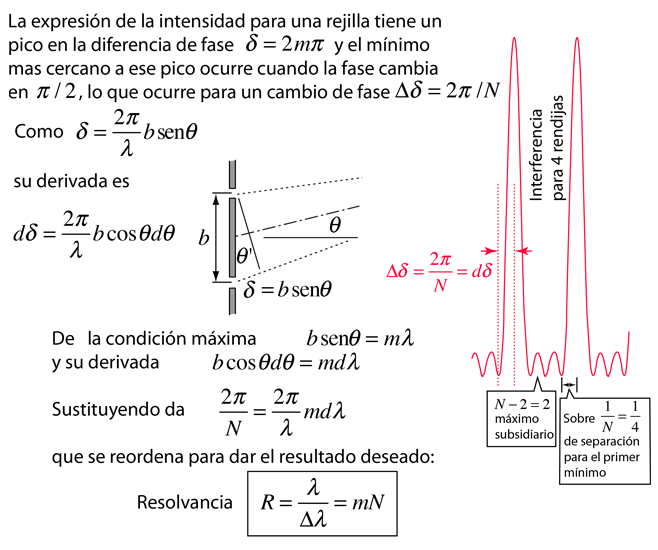
La resolvancia o "poder de resolución cromática" de un dispositivo que se usa para separarar las longitudes de onda de luz, se define como

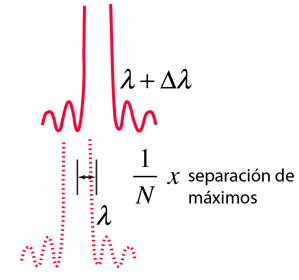
El límite de la resolución está determinado por el criterio de Rayleigh cuando se aplica sobre la máxima difracción, es decir; dos longitudes de ondas están justamente resueltas, cuando el máximo de una, se encuentra con el primer mínimo de la otra.
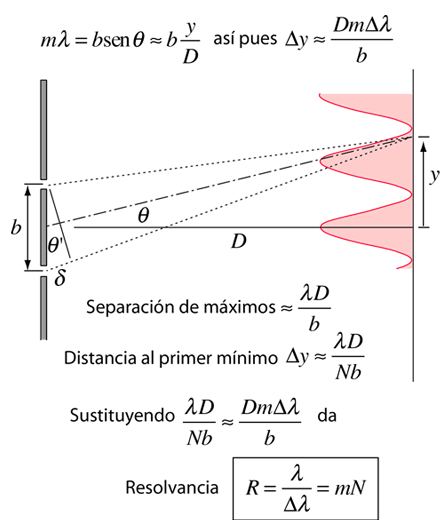
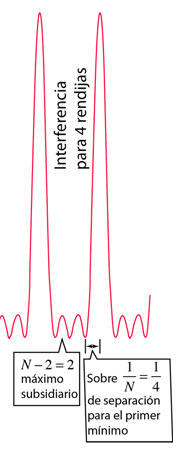
Dado que el espacio entre los máximos de N rendijas se divide en N-2 máximos subsidiarios, la distancia al primer mínimo es esencialmente 1/N veces la distancia entre los máximos principales. Esto lleva a una resolvancia de rejilla de
donde N es el número total de ranuras iluminadas y m es el orden de difracción. |
 |
Conceptos de Red de Difracción
| HyperPhysics*****Luz y Visión | M Olmo R Nave |