Modelación de la Semi Vida de la Partícula Alfa del Polonio-212
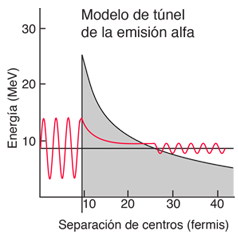 |
Para modelar la penetración de barrera que conduce a la emisión alfa del polonio-212, se debe calcular un determinado número de parámetros. Se asume que la influencia nuclear se detiene bruscamente, cuando la partícula alfa emitida, y el reducido núcleo apenas se toquen entre sí. Usando la fórmula del radio nuclear, esta distancia para el polonio-212 es 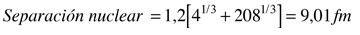 La altura de la barrera a la distancia de arriba, se calcula como potencial de Coulomb de cargas puntuales. Por la emisión alfa, la carga del núcleo restante se ha reducido en dos, de modo que la altura de barrera V(a) es: 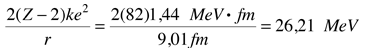 |
La distancia a la que el potencial de Coulomb cae al nivel de energía de la partícula alfa de polonio-212 observado, es
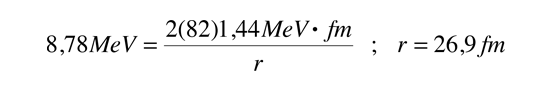
Así pues, el ancho de la barrera es
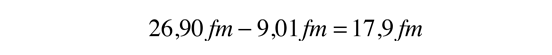
Además de la probabilidad de efecto tunel de abajo, la tasa de emisión alfa depende de cuántas veces una partícula alfa con esta energía dentro del núcleo, llegue a las paredes. La velocidad de la partícula alfa puede calcularse a partir de
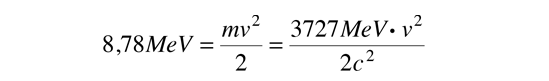
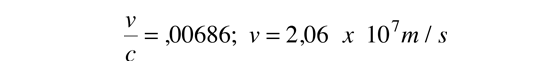
ya que una partícula alfa con esta energía no es relativista. La frecuencia de golpear las paredes es entonces
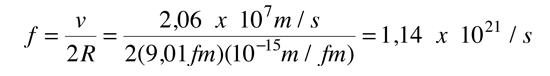
Sólo con objeto de comparación, se calculará la semi vida esperada para una simple barrera rectangular igual a la altura del pico de la barrera. La probabilidad de efecto túnel para una barrera rectangular de altura 26,2 MeV, y una anchura de 17,9 fm, es

Para una partícula alfa determinada, la probabilidad por segundo de emisión es el producto
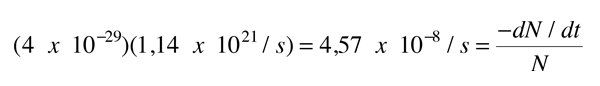
que se puede usar en la fórmula del decaimiento nuclear, para obtener la semi vida
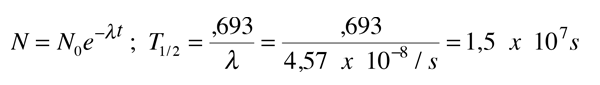
Obviamente, esto no es una buena aproximación -¡¡se pierden 13 órdenes de magnitud!!-.
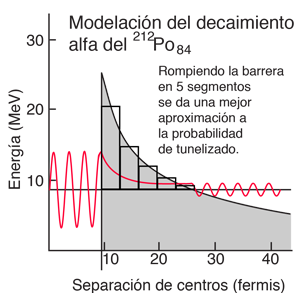 |
Se podría obtener una mejor probabilidad de efecto túnel, troceando la barrera en cinco segmentos, y multiplicando las sucesivas probabilidades de efecto túnel. Se construyó la tabla siguiente, mediante la división del ancho de 17,9 fm en cinco segmentos iguales, con una altura igual a la altura del punto medio del segmento.
|
Para una partícula alfa determinada, la probabilidad de efecto túnel combinado por segundo de emisión, es el producto
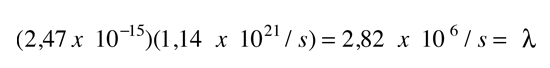
que da la semi vida
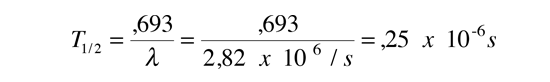
Así que el modelo da una semi vida de 0,25 microsegundos en comparación con la semi vida experimental de 0,3 microsegundos. ¡No está mal!. Pero hay que admitir que este es un ejemplo fortuito. No todos ellos están de acuerdo así de bien, con tan sólo una aproximación de cinco segmentos de barrera. Krane en la sección 8.4 presenta y demuestra un enfoque integral para calcular la barrera en lugar de solo un número finito de segmentos. Incluso esta sofisticación no siempre concuerda bien con la vida media porque hay complicaciones del entorno nuclear como núcleos no esféricos. Sin embargo, tal tunelización de la mecánica cuántica muestra concordancia con la amplia gama de semividas de la desintegración alfa, ¡que abarcan más de 20 órdenes de magnitud!
| Estudio del Decaimiento Alfa del Polonio |
| Aplicar el Modelo a Otros Emisores de Partículas Alfa |
Referencias
Rohlf
Sec 7-4
Eisberg & Resnick
Sec 16-2
Krane
Sec 8.4
| HyperPhysics*****Nuclear | M Olmo R Nave |