 |
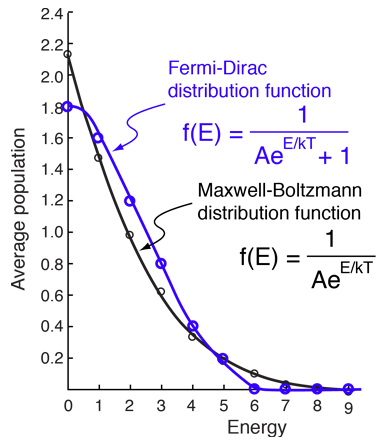
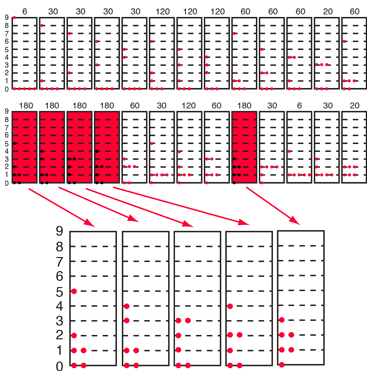
How many ways can you distribute 9 units of energy among 6 identical, indistinguishable fermions?Fermi-Dirac statistics differ dramatically from the classical Maxwell-Boltzmann statistics in that fermions must obey the Pauli exclusion principle. Considering the particles in this example to be electrons, a maximum of two particles can occupy each spatial state since there are two spin states each. Whereas there were 26 possible configurations for distinguishable particles, these are reduced to the 5 states which have no more than two particles in each state. |
Evaluating the average occupancy of each energy state is much simpler than in the Maxwell-Boltzmann example since each macrostate has a weight of 1. The average occupancy is just the sum of the numbers of particles in a given energy state over all the 5 distributions divided by 5.
| Evaluate the average for each energy state. | Compare with Maxwell-Boltzmann example. |
Reference
Blatt
Ch. 11
| HyperPhysics***** Quantum Physics | R Nave |