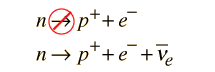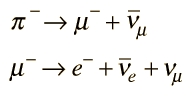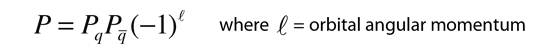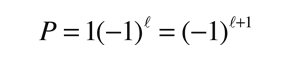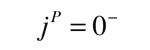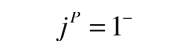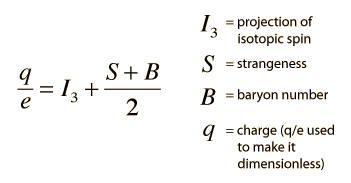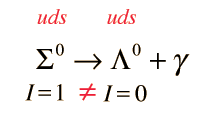Particle Interactions and Conservation Laws

In developing the standard model for particles, certain types of interactions and decays are observed to be common and others seem to be forbidden. The study of interactions has led to a number of conservation laws which govern them. These conservation laws are in addition to the classical conservation laws such as conservation of energy, charge, etc., which still apply in the realm of particle interactions. Strong overall conservation laws are the conservation of baryon number and the conservation of lepton number. Specific quantum numbers have been assigned to the different fundamental particles, and other conservation laws are associated with those quantum numbers.

From another point of view, it would seem that any localized particle of finite mass should be unstable, since the decay into several smaller particles provides many more ways to distribute the energy, and thus would have higher entropy. This idea is even stated as a principle called the "totalitarian principle" which might be stated as "every process that is not forbidden must occur". From this point of view, any decay process which is expected but not observed must be prevented from occurring by some conservation law. This approach has been fruitful in helping to determine the rules for particle decay.

Conservation laws for parity, isospin, and strangeness have been developed by detailed observation of particle interactions. The combination of charge conjugation (C), parity (P) and time reversal (T) is considered to be a fundamental symmetry operation - all physical particles and interactions appear to be invariant under this combination. Called CPT invariance, this symmetry plumbs the depths of our understanding of nature.

Another part of the high energy physicist's toolkit in anticipating what interactions can be expected is "crossing symmetry". Any interaction which is observed can be used to predict other related interactions by "crossing" any particle across the reaction symbol and turning it into its antiparticle.

Conservation of Baryon Number

Nature has specific rules for particle interactions and decays, and these rules have been summarized in terms of conservation laws. One of the most important of these is the conservation of baryon number. Each of the baryons is assigned a baryon number B=1. This can be considered to be equivalent to assigning each quark a baryon number of 1/3. This implies that the mesons, with one quark and one antiquark, have a baryon number B=0. No known decay process or interaction in nature changes the net baryon number.

The neutron and all heavier baryons decay directly to protons or eventually form protons, the proton being the least massive baryon. This implies that the proton has nowhere to go without violating the conservation of baryon number, so if the conservation of baryon number holds exactly, the proton is completely stable against decay. One prediction of grand unification of forces is that the proton would have the possibility of decay, so that possibility is being investigated experimentally.

Conservation of baryon number prohibits a decay of the type

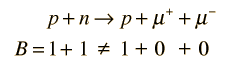
but with sufficient energy permits pair production in the reaction

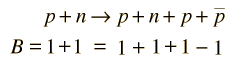
The fact that the decay

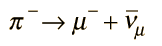
is observed implied that there is no corresponding principle of conservation of meson number. The pion is a meson composed of a quark and an antiquark, and on the right side of the equation there are only leptons. (Equivalently, you could assign a baryon number of 0 to the meson.)

Conservation of Lepton Number

Nature has specific rules for particle interactions and decays, and these rules have been summarized in terms of conservation laws. One of the most important of these is the conservation of lepton number. This rule is a little more complicated than the conservation of baryon number because there is a separate requirement for each of the three sets of leptons, the electron, muon and tau and their associated neutrinos.

The first significant example was found in the decay of the neutron. When the decay of the neutron into a proton and an electron was observed, it did not fit the pattern of two-particle decay. That is, the electron emitted does not have a definite energy as is required by conservation of energy and momentum for a two-body decay. This implied the emission of a third particle, which we now identify as the electron antineutrino.

The assignment of a lepton number of 1 to the electron and -1 to the electron antineutrino keeps the lepton number equal to zero on both sides of the second reacton above, while the first reaction does not conserve lepton number.

The observation of the following two decay processes leads to the conclusion that there is a separate lepton number for muons which must also be conserved.

The first reaction above (decay of the pion) is known to be a two-body decay by the fact that a well-defined muon energy is observed from the decay. However, the decay of the muon into an electron produces a distribution of electron energies, showing that it is at least a three-body decay. In order for both electron lepton number and muon lepton number to be conserved, then the other particles must be an electron anti-neutrino and a muon neutrino.

Parity

One of the conservation laws which applies to particle interactions is associated with parity.

Quarks have an intrinsic parity which is defined to be +1 and for an antiquark parity = -1. Nucleons are defined to have intrinsic parity +1. For a meson with quark and antiquark with antiparallel spins (s=0), then the parity is given by

The meson parity is given by

The lowest energy states for quark-antiquark pairs (mesons) will have zero spin and negative parity and are called pseudoscalar mesons. The nine pseudoscalar mesons can be shown on a meson diagram. One kind of notation for these states indicates their angular momentum and parity

Excited states of the mesons occur in which the quark spins are aligned, which with zero orbital angular momentum gives j=1. Such states are called vector mesons.

The vector mesons have the same spin and parity as photons.

All neutrinos are found to be "left-handed", with an intrinsic parity of -1 while antineutrinos are right-handed, parity =+1.

Isospin

Isospin is a term introduced to describe groups of particles which have nearly the same mass, such as the proton and neutron. This doublet of particles is said to have isospin 1/2, with projection +1/2 for the proton and -1/2 for the neutron. The three pions compose a triplet, suggesting isospin 1. The projections are +1 for the positive, 0 and -1 for the neutral and negative pions. Isospin is used as an axis in particle diagrams, with strangeness being the other axis. Isospin is not really spin, and doesn't have the units of angular momentum - the spin term is tacked on because the addition of the isospins follows the same rules as spin.

Isospin is a dimensionless quantity associated with the fact that the strong interaction is independent of electric charge. Any two members of the proton-neutron isospin doublet experience the same strong interaction: proton-proton, proton-neutron, neutron-neutron have the same strong force attraction.

At the quark level, the up and down quarks form an isospin doublet (I=1/2) and the projection I₃ = +1/2 is assigned to the up quark and I₃ =-1/2 to the down. (The subscript 3 is used here for the third component rather than the z used with spin and orbital angular momentum because most of the literature does so.) The other quarks are assigned isospin I=0. Isospin is related to other quantum numbers for the particles by

This relationship is called the Gell Mann-Nishijima formula. Some references use T for isospin, but it appears that most use I for isospin and T for weak isospin.

Isospin is associated with a conservation law which requires strong interaction decays to conserve isospin, as illustrated by the process

which does not involve any transmutation of quarks, so would be expected to decay by strong interaction. However, it does not conserve isospin, and is observed to decay by the electromagnetic interaction, but not by the strong interaction. The experimental discrimination is made by the observation of its decay lifetime, presuming by the totalitarian principle that if it could decay by the strong interaction, it would.