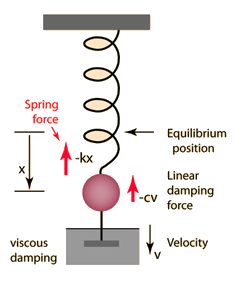
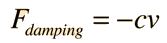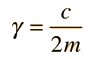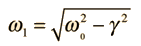Damped Harmonic Oscillator
|
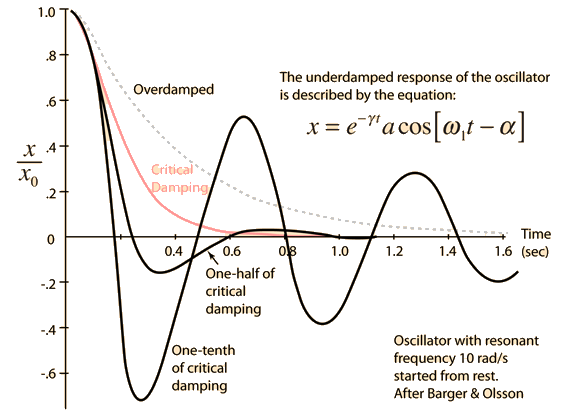
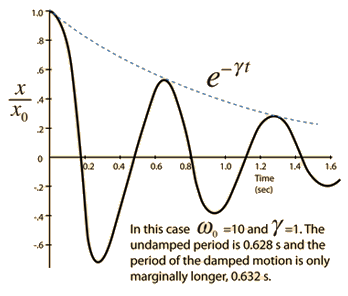
The Newton's 2nd Law motion equation is 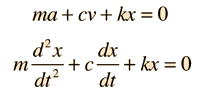 This is in the form of a homogeneous second order differential equation and has a solution of the form 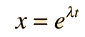 Substituting this form gives an auxiliary equation for λ 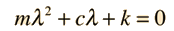 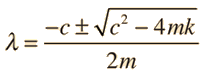 The three resulting cases for the damped oscillator are
|
Periodic motion concepts
| HyperPhysics***** Mechanics | R Nave |