Einstein A and B Coefficients

In 1917, about 9 years before the development of the relevant quantum theory, Einstein postulated on thermodynamic grounds that the probability for spontaneous emission, A, was related to the probability of stimulated emission, B, by the relationship

From the development of the theory behind blackbody radiation, it was known that the equilibrium radiation energy density per unit volume per unit frequency was equal to

Einstein argued that equilibrium would be possible, and the laws of thermodynamics obeyed, only if the ratio of the A and B coefficients had the value shown above. This ratio was calculated from quantum mechanics in the mid 1920's. In recognition of Einstein's insight, the coefficients have continued to be called the Einstein A and B coefficients.

While applicable in many situations, the A and B coefficients received particular attention in the period in which lasers were being developed. The nature of the coefficients is such that you cannot use the radiation in a cavity to elevate electrons preferentially into an upper state, producing the population inversion necessary for laser action. The particular ratio between the coefficients suggests that the presence of the light to "pump" electrons into upper states will have the same probability of stimulating an already elevated electron to make the downward transition, so that laser action cannot be achieved with any two-level system. The achievement of laser action was obtained by three-level systems like that in the helium-neon laser where the population of the upper neon level could be achieved by a non-radiative transfer from the helium gas pumping energy to the neon atoms.

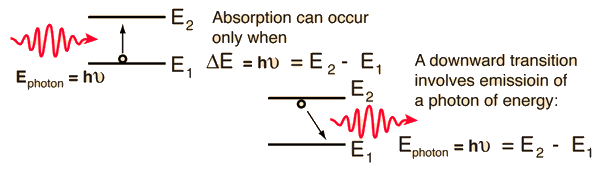
The implication of the Einstein A and B coefficients is that these two processes will occur at equal rates, so that no population inversion can be attained in a two-level system like that depicted here. In the helium-neon laser, for example, this limitation is overcome by collisional transfer from the helium gas to the neon gas, achieving the necessary population inversion for laser action.