System Matrix: Two Thin Lenses

The position of the image formed by a pair of thin lenses can be found by the matrix method. The general matrix method involves multiplying a vector form of the incident vergence successively by matrices representing (1)the refraction by the first lens, (2) the translation to the second lens, and (3) the refraction by the second lens. If the system matrix is calculated, it can be used to directly multiply the incident vergence to obtain the exit vergence. From that exit vergence the image distance is calculated.

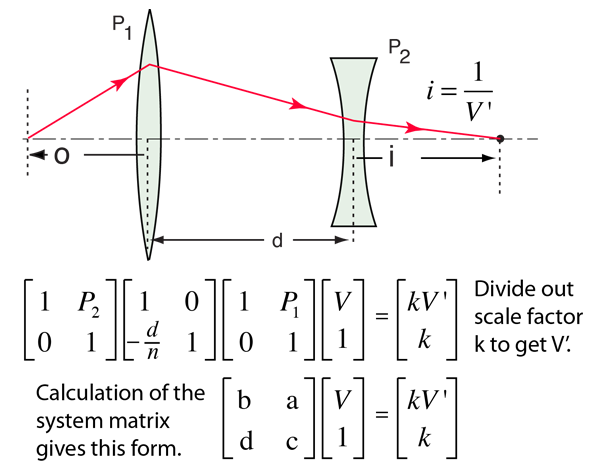
This example is for a two thin lenses surrounded by air (n=1). It involves the powers of the lens and the separation d of the lenses. It also involves the principal planes H₁ and H₂. As with most ordinary geometrical optics, it is applicable only for small angles (paraxial rays). The development also follows the cartesian sign convention.

A default set of values for the parameters of this calculation is provided. You can see the default calculation by entering a 0 into one of the lens parameters, which will trigger the entry of the default parameters for the lenses. Any of them may be then changed to explore the behavior of the lens system.

The power for lens 1 is P₁ = m^-1

The power for lens 2 is P₂ = m^-1

The lens separation d = m

The symbols used by Meyer-Arendt for the elements of the system matrix will be used. b = a = d = c =

****************

A number of other characteristics of the thick lens may be calculated from the system matrix.

The right-hand, or equivalent focal length of the lens is just the reciprocal of matrix element a: f₂ = 1/a = m.

The distance V₂H₂ from the right vertex to the associated principal plane is given by V₂H₂= (c-1)/a = m.

The right vertex focal length (or back focal length) is given by f_v2 = c/a = m.

Note that the equivalent focal length f₂ is the sum of the back vertex focal length and the distance from the vertex to the principal plane: f₂ = f_v2 + V₂H₂. Similar relationships exist for the left-hand or front vertex.

The left vertex focal length (or front focal length) is given by f_v1 = -b/a = m.

The distance V₁H₁ from the left vertex to the associated principal plane is given by V₁H₁= (1-b)/a = m.

The equivalent front focal length f₁ is then given by f₁ = -(b/a + V₁H₁) = m. ****************************

Location of Image with System Matrix

Reminder: Using the Cartesian sign convention, the object distance is typically a negative number since it points opposite to the direction of light travel.

For object* distance o = m, the value of the input vergence V = . Performing the indicated matrix multiplication gives: kV'= k=. Dividing both by k gives the exit vergence V' = m-1 so the image distance i = m.

Note that the calculation does not take into account the change in lens separation with the angle of the incoming ray. It is typical to do the calculation only for the paraxial rays where the departure from full separation is negligible.