Image from System Matrix
The position of the image formed by a thick lens can be found by using the system matrix. This involves multiplying a vector form of the incident vergence successively by three matrices representing (1)the refraction by the first surface, (2)the translation to the second surface, and (3) the refraction by the second surface. Those three operations can be combined to form the system matrix. The entrance vergence can then be just multiplied times the system matrix to determine the exit vergence and from that vergence, the image distance is calculated.
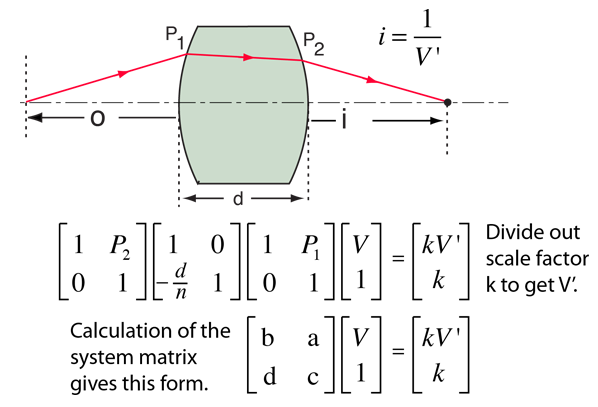
The example is for a lens with index of refraction n surrounded by air (n=1). It involves the surface powers of the lens and the thickness d between the vertexes. It also involves the principal planes H1 and H2. As with most ordinary geometrical optics, it is applicable only for small angles (paraxial rays). The development also follows the cartesian sign convention.
*Using the Cartesian sign convention, the object distance is typically a negative number since it points opposite to the direction of light travel. The input vergence is therefore negative (divergent).
The equivalent power for the thick lens can be calculated from Gullstrand's equation:
Note that the calculation does not take into account the change in lens thickness with the angle of the incoming ray. It is typical to do the calculation only for the paraxial rays where the departure from full thickness is negligible.
| Vergence Example | Matrix definitions | Example for two thin lenses |
Lens concepts
Thick lens concepts
| HyperPhysics***** Light and Vision | R Nave |