Second Order Non-homogeneous Differential Equation

Many physical problems involve second order differential equations. Some applications involve homogeneous equations, but the more general case is the non-homogeneous equation. The general form of the second order differential equation is

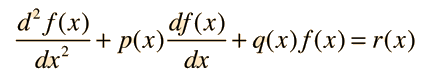
The path to a general solution involves finding a solution f_h(x) to the homogeneous equation, and then finding a particular solution f_p(x) to the non-homogeneous equation (i.e., find any solution that satisfies the equation with all terms included). The form of the general solution is

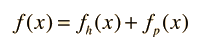
A great variety of types of solutions arise in physical problems and specific functions arise, depending upon the boundary conditions.