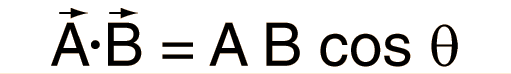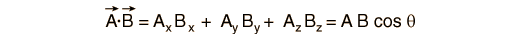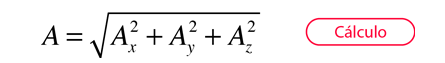Producto Escalar de Vectores
El producto escalar y el producto vectorial son las dos formas de multiplicar vectores que vemos en la mayoría de las aplicaciones de Física y Astronomía. El producto escalar de dos vectores se puede construir, tomando la componente de un vector en la dirección del otro vector y multiplicandola por la magnitud del otro vector. Esto se puede expresar de la forma:

Si se expresan los vectores en términos de los vectores unitarios i, j, y k a lo largo de las direcciones x, y, y z, el producto escalar, tambien se puede expresar de la forma:
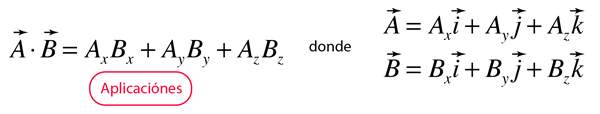
Conceptos de Vector
| HyperPhysics*****Mecánica | M Olmo R Nave |