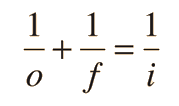Ecuación de Lentes Delgadas
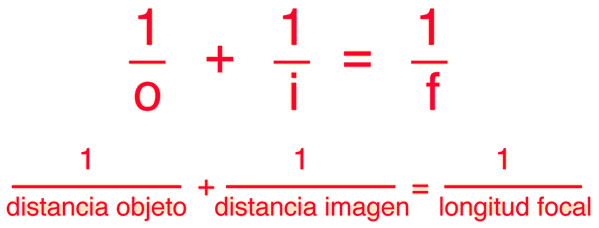
Abajo se muestra la forma común Gausiana de la ecuación de lentes. Esta es la forma que se usa en la mayoría de los textos introductorios. La forma usando la convención de signos cartesianos, se utiliza a menudo en los textos mas avanzados, debido a la ventaja que ofrece con los sistemas de múltiples lentes e instrumentos ópticos mas complejos. Cualquiera de las formas se pueden usar con lentes positivas o negativas y predicen la formación de ambas imágenes real y virtual. No se aplica a las lentes gruesas.
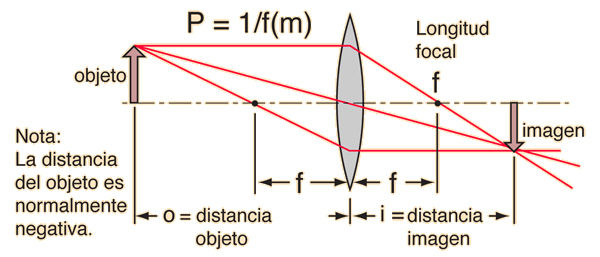
Si de la ecuación de lentes resulta una distancia de imagen negativa, entonces se trata de una imagen virtual en el mismo lado de la lente donde está el objeto. Si resulta una longitud focal negativa, entonces se trata de una lente divergente en vez de una lente convergente como la de la ilustración. Se puede usar la ecuación de lente para calcular la distancia de la imagen, tanto para una imagen real como virtual, y tanto para lentes positivas como negativas. La fórmula del aumento lineal, permite predecir el tamaño de la imagen.
| Fórmula de la Ecuación de Lentes con la Convención de Signos Cartesianos |
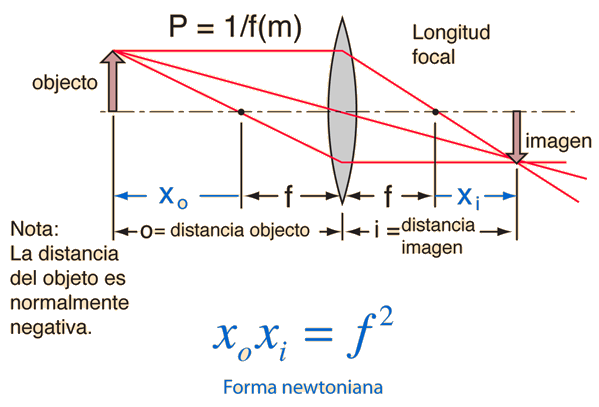
| Reversibilidad de los Puntos del Objeto y la Imagen: Puntos Conjugados |
Conceptos sobre Lentes
| HyperPhysics*****Luz y Visión | M Olmo R Nave |