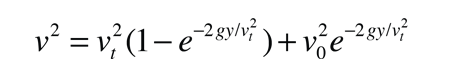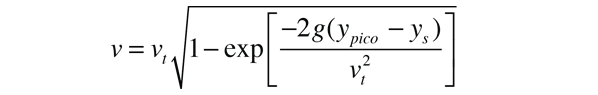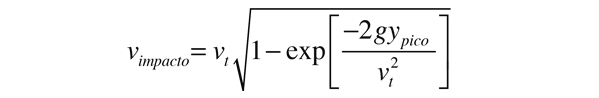Velocidad de Caída Libre vs Distancia en Arrastre Cuadrático

Se presumirá que un objeto que cae libremente experimenta una fuerza de resistencia del aire proporcional al cuadrado de su velocidad. La dirección hacia abajo se tomará como positiva, y el objeto del cálculo es la velocidad en función de la distancia y, para un objeto caído del reposo. Las expresiones se desarrollarán para las dos formas de resistencia del aire que se utilizarán para las trayectorias.

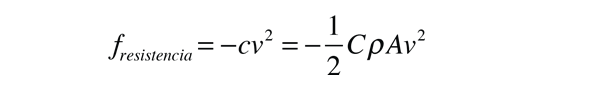
La velocidad de caída libre en función del tiempo si se cae del reposo viene dada por

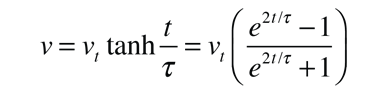
Esta ecuación se puede convertir en una en la que la variable independiente sea la distancia en lugar del tiempo haciendo uso de la expresión

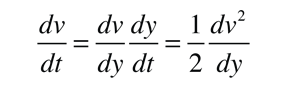
Esto se puede usar para reescribir la ecuación del movimiento anterior como

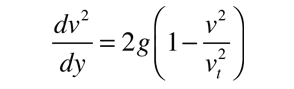
Esta ecuación se resuelve mediante el siguiente procedimiento:

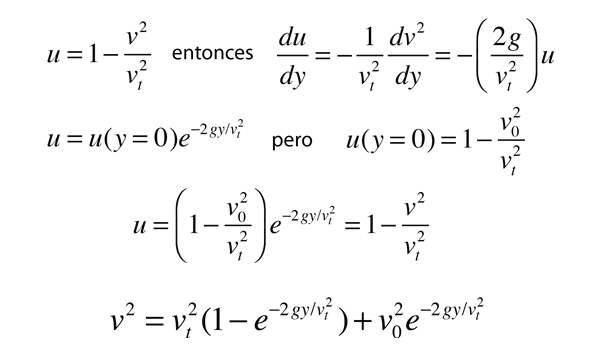
Esto expresa la velocidad de caída libre v en términos de la distancia de caída y. Tiene dos términos de disminución exponencial para que después de una distancia de caída suficiente, la velocidad sea esencialmente la velocidad terminal v_t. Una longitud característica v_t²/2g expresa una distancia donde la velocidad se aproxima a v_t.

Velocidad de Caída Libre vs Altura en Arrastre Cuadrático

Se presumirá que un objeto que cae libremente experimenta una fuerza de resistencia del aire proporcional al cuadrado de su velocidad. La dirección hacia abajo se tomará como positiva, y la velocidad en función de la altura y_s para un objeto caído desde una altura máxima y_peak es el objeto del cálculo. Téngase en cuenta que y_s se está utilizando como la altura sobre la superficie en este caso, por lo que no es lo mismo que la y en el desarrollo anterior. A partir de ese desarrollo anterior, la velocidad en función de la distancia de caída desde la altura máxima está dada por

donde y = y_peak - y_s. Para esta aplicación v₀=0 ya que la velocidad es cero en la altura del pico. La expresión para v entonces se convierte en

La velocidad en el impacto se puede obtener para y_s=0:

Estas expresiones se usan en el cálculo de la trayectoria vertical.