Puntos de Lagrange del Sistema Tierra-Luna

Un sistema mecánico con tres objetos, por ejemplo la Tierra, la Luna y el Sol, constituye un problema de tres cuerpos. El problema de tres cuerpos es famoso tanto en los círculos de las matemáticas como la física, y los matemáticos en la década de 1950 lograron finalmente una prueba elegante de que es imposible resolver el problema. Sin embargo, las soluciones aproximadas pueden ser muy útiles, sobre todo cuando las masas de los tres objetos son muy diferentes.

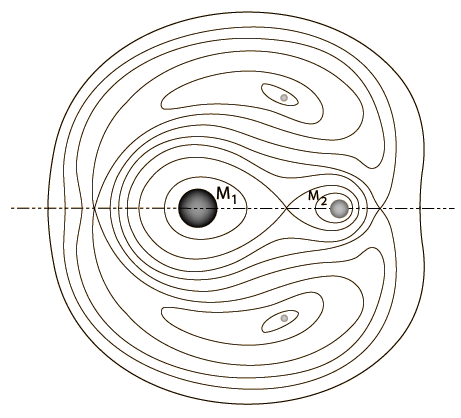
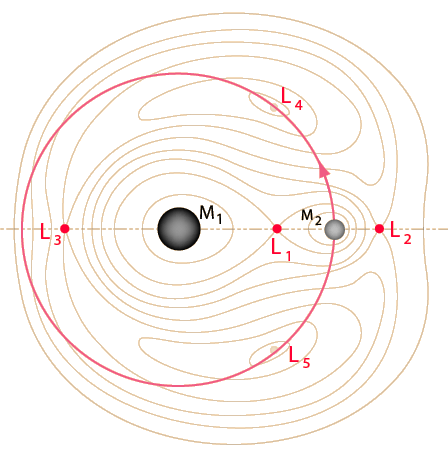
Para el sistema Sol-Tierra-Luna, la masa del Sol es tan dominante que puede ser tratada como un objeto fijo y el sistema Tierra-Luna tratado como un sistema de dos cuerpos desde el punto de vista de un marco de referencia que orbita alrededor del Sol. Los matemáticos del siglo 18, Leonhard Euler y Joseph-Louis Lagrange descubrieron que existen cinco puntos especiales en este marco de referencia rotatorio, donde se podría mantener un equilibrio gravitacional. Es decir, un objeto colocado en cualquiera de estos cinco puntos en el marco rotatorio, podría permanecer allí con las fuerzas efectivas con respecto a este marco canceladas. Tal objeto podría entonces, orbitar el Sol, manteniendo la misma posición relativa con respecto al sistema Tierra-Luna. Estos cinco puntos son llamados puntos de Lagrange y numerados de L1 a L5.

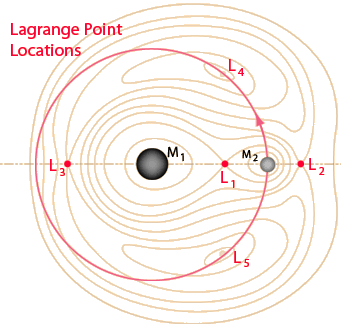Los puntos de Lagrange L4 y L5 constituyen puntos de equilibrio estable, de modo que un objeto colocado alli, estaría en una órbita estable con respecto a la Tierra y la Luna. Con pequeñas salidas del L4 o L5, habría una fuerza de restauración efectiva, para regresar el satélite al punto estable.

El punto L5 fué objeto de una gran propuesta para fundar una colonia en "The High Frontier" por Gerard K. O'Neill y se hizo un gran esfuerzo en la década de 1970 para trabajar en los detalles de ingeniería para la creación de tal colonia. Hubo una activa "Sociedad L5" que promocionó las ideas de O'Neill. Los puntos L4 y L5 forman un triángulo equilátero con el Sol y el sistema Tierra-Luna.

Los puntos de Lagrange L1, L2 y L3 no parece ser tan útiles porque son puntos de equilibrio inestable. Al igual que el equilibrio de un lápiz apoyado sobre su punta, mantener un satélite en esos puntos, es teoricamente posible, pero cualquier influencia perturbadora, lo puede llevar fuera del equilibrio. Sin embargo, en la práctica se ha probado que estos puntos de Lagrange son realmente muy útiles ya que podemos poner un satélite orbitando uno de estos puntos con muy poco gasto de energía. Estos puntos, han proporcionado lugares útiles para estacionar un vehículo espacial para las observaciones. Estas órbitas alrededor de L1 y L2 son a menudo llamadas órbitas de halo. L3 se encuentra en el lado opuesto del Sol desde la Tierra, por lo que no es tan fácil de usar. Podría ser un buen lugar para esconder algo, ya que nunca sería visto. -¡un terreno fértil para la ciencia ficción!-.

El punto de Lagrange L2 se ha utilizado para el Wilkinson Microwave Anisotropy Probe (WMAP). Como L2 está posicionado fuera de la órbita de la Tierra, la WMAP, puede encarar al mismo tiempo el Sol y la Tierra, una característica importante de la sonda del espacio profundo, que puede emplear detectores ultra-sensibles, sin peligro de cegarse mirando al Sol o la Tierra.

Las Superficies Equipotenciales de tres Cuerpos

Un sistema mecánico con tres objetos, por ejemplo la Tierra, la Luna y el Sol, constituye un problema de tres cuerpos. El problema de tres cuerpos es famoso tanto en los círculos de las matemáticas como la física, y los matemáticos en la década de 1950 lograron finalmente una prueba elegante de que es imposible resolver el problema. Sin embargo, las soluciones aproximadas pueden ser muy útiles, sobre todo cuando las masas de los tres objetos son muy diferentes.

Las contribuciones de Lagrange fué, dibujar el contorno de igual energía potencial gravitacional en sistemas donde la tercera masa era muy pequeña en comparación con las otras dos. A continuación se presenta un esbozo de tales contornos equipotenciales para un sistema como el sistema Tierra-Luna. El contorno equipotencial, que dibuja una figura de 8 alrededor de ambas masas, es importante en la evaluación de escenarios donde una parte pierde masa que va hacia la otra. Estos bucles equipotenciales, forma la base para el concepto del lóbulo Roche.

Contornos de Potencial Gravitacional Iguales

Una de las observaciones de Lagrange de los contornos potenciales, era que había cinco puntos en los que el tercer cuerpo podría estar en equilibrio, los puntos que ahora son llamados puntos de Lagrange.

Los Puntos de Lagrange para un Sistema como el de Tierra-Luna

Los puntos de Lagrange L₁, L₂, y L₃ son puntos de equilibrio inestable. Al igual que el equilibrio de un lápiz apoyado sobre su punta, mantener un satélite en esos puntos, es teoricamente posible, pero cualquier influencia perturbadora, lo puede llevar fuera del equilibrio. Cabe destacar que los puntos de Lagrange L₄ y L₅ para pequeñas masas, son puntos de equilibrio estable en el sistema de tres cuerpos y esta geometría de los tres cuerpor puede mantenerse, mientras M₂ orbita alrededor de M₁.

Joseph Louis Lagrange

Lagrange fué un matemático del siglo 18 que abordó el famoso problema de tres cuerpos a finales de los años 1700. El problema no puede resolverse con exactitud, pero el encontró con que en el caso de que el tercer cuerpo sea muy pequeño en comparación con los otros dos, algunas soluciones útiles aproximadas.