Vector Calculus Operations
Three vector calculus operations which find many applications in physics are:
1. The divergence of a vector function
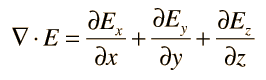
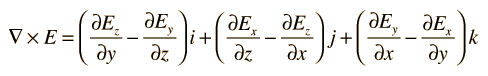
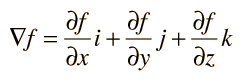
Vector calculus
| HyperPhysics*****HyperMath*****Calculus | R Nave |
Vector CalculusMany quantities which are of interest in physics are both directed quantities (vectors) and can take on a continuous range of values, making calculus methods necessary. Several operations from the mathematical field of vector calculus are of particular importance in solving physical problems.
|
Index Vector concepts | ||||
|
Go Back |
Vector Calculus OperationsThree vector calculus operations which find many applications in physics are: 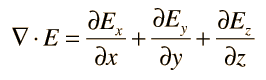 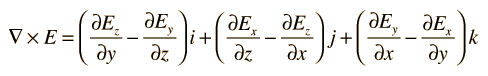 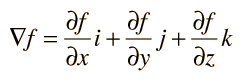 |
Index Vector calculus | ||
|
Go Back |
The Del OperatorThe collection of partial derivative operators 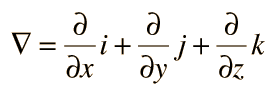
|
Index Vector calculus | ||||||||
|
Go Back |