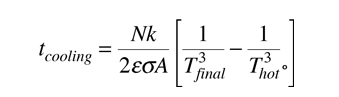Radiative Cooling of a Volcanic Fragment
The radiative cooling time for the ideal case of an object which remains at a uniform temperature with no limitation from heat transfer from the interior of the object is given by :
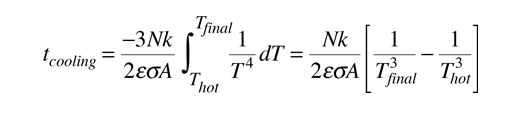
It must be kept in mind that for macroscopic objects, the calculated cooling time for the object as a whole will always be shorter than the real cooling time, so that it gives a lower bound. The above relationship assumes infinite thermal conductivity so that the temperature of the whole object is equal to the surface temperature. In the real world, the surface will cool faster than the interior. The rate of heat transfer from the interior will be expected to limit the rate of radiative loss from the surface.
Despite all these real-world limitations, it is interesting to try to model the process of the cooling of a hot object. Dr. Pam Burnley of GSU's Geology Department has a fragment of basaltic material which she found some 60 meters from the top of a small volcanic cone. The material has the appearance of having been ejected in an almost liquid state, but upon impact,it just bent one end of the fragment. This seems to imply that during its flight out of the cone, it cooled enough to be partially solid before impact.

 |
These two views of the fragment show the two sides and the general impression of something fairly soft which was bent upon impact. It looks like a kind of splash of the volcanic material. Dr. Burnley refers to it as a "bomb" from the volcano. |
Basic data was collected for the sample. Its mass is 367.6 grams. It measured about 17cm long, 5.5cm across and about 3.5cm thick. Submerged in water, its effective mass was 161 grams, so by Archimedes principle, its volume is 206.6 cm3. This gives a density of 1.78 gm/cm3, compared to a density of about 3 gm/cm3 for solid basalt, so there is a lot of air in it. Dr. Burnley estimated temperatures of about 1200 °C for the liquidus for this material and about 1000 °C for its solidus. So those seem to be plausible temperatures to use as the hot and cold temperatures for this modeling process.
| Modeling the Radiative Cooling of a Hot Sphere |
| Kelvin Cooling Time for the Earth |
| HyperPhysics***** Thermodynamics | R Nave |