Wien's Displacement Law and Other Ways to Characterize the Peak of Blackbody Radiation
When the temperature of a blackbody radiator increases, the overall radiated energy increases and the peak of the radiation curve moves to shorter wavelengths. When the maximum is evaluated from the Planck radiation formula, the product of the peak wavelength and the temperature is found to be a constant.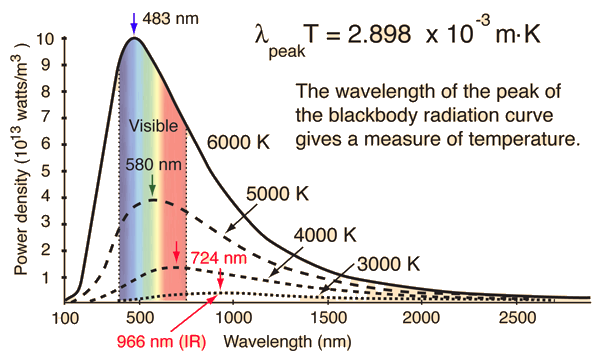
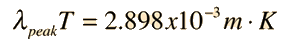
This relationship is called Wien's displacement law and is useful for the determining the temperatures of hot radiant objects such as stars, and indeed for a determination of the temperature of any radiant object whose temperature is far above that of its surroundings. The temperature can be found from the wavelength at which the radiation curve peaks.
It should be noted that the peak of the radiation curve in the Wien relationship is the peak only because the intensity is plotted as a function of wavelength. If frequency or some other variable is used on the horizontal axis, the peak will be at a different wavelength.
There are various rationales for using the alternate ways of plotting the blackbody radiation curve, as discussed by Heald. The process of finding the maximum in a given presentation is to set the derivative of the intensity equal to zero and then numerically solve the transcendental equation that results. The solutions for the processes included above are summarized below.

| The original Wien displacement law is the maximum of the blackbody spectrum plotted against linear wavelength, a presentation appropriate for experiments with diffraction gratings. This kind of plot puts the peak of the Sun's spectrum near the 550nm peak of the sensitivity of human vision. But the peak of a plot against linear frequency puts the peak at 880nm in the infrared, and the plot against linear frequency seems just as logical. The frequency-squared alternative would be appropriate for experiments using prisms. The logarithmic plot gives equal intensity per percentage bandwidth, and the median rule puts the peak in a position where there is equal intensity on each side of the peak. |
spectrum | ||
| Electromagnetic Spectrum | Photon Quantum Energy |
Blackbody radiation concepts
Reference
Heald
| HyperPhysics***** Quantum Physics | R Nave |