Rutherford Scattering Questions
Rutherford concepts
Scattering concepts
| HyperPhysics***** Nuclear | R Nave |
History of Rutherford ExperimentIn Ernest Rutherford's laboratory, Hans Geiger and Ernest Marsden (a 20 yr old undergraduate student) carried out experiments to study the scattering of alpha particles by thin metal foils. In 1909 they observed that alpha particles from radioactive decays occasionally scatter at angles greater than 90°, which is physically impossible unless they are scattering off something more massive than themselves. This led Rutherford to deduce that the positive charge in an atom is concentrated into a small compact nucleus. During the period 1911-1913 in a table-top apparatus, they bombarded the foils with high energy alpha particles and observed the number of scattered alpha particles as a function of angle. Based on the Thomson model of the atom, all of the alpha particles should have been found within a small fraction of a degree from the beam, but Geiger and Marsden found a few scattered alphas at angles over 140 degrees from the beam. Rutherford's remark "It was quite the most incredible event that ever happened to me in my life. It was almost as incredible as if you had fired a 15-inch shell at a piece of tissue paper and it came back and hit you." The scattering data was consistent with a small positive nucleus which repelled the incoming positively charged alpha particles. Rutherford worked out a detailed formula for the scattering (Rutherford formula), which matched the Geiger-Marsden data to high precision. The source used in the Rutherford experiments was purifed radium contained in a thin-walled 1-mm diameter glass tube. The source strength was about 0.1 Curie, or about 4 billion nuclear decays per second. The alpha particles were allowed to pass through a small diaphragm and were directed toward a thin foil target. The detector was a small (10-6 m2) zinc sulfide screen mounted a few centimeters away from the target. (Rohlf) |
Index Rutherford concepts References Rohlf Ch 6 Blatt Ch 5 | ||
|
Go Back |
Geiger-Marsden Data on Alpha Scattering
Since they had used the most energetic alpha particles at their disposal, 7.7 MeV, and still hadn't seen the departure from Coulomb scattering which would signal a direct interaction with the nucleus, they had to look for other alternatives to get a measure of nuclear size. This led to a famous remark by Rutherford to his graduate students "There is no money for apparatus -. we shall have to use our heads!"(Keller) The form that "using their heads" took was the study of lighter target nuclei, and finally the use of aluminum target nuclei yielded measurable direct backscatter of alpha particles, at least establishing an upper bound for the nuclear size.
|
Index Rutherford concepts Scattering concepts | ||||
|
Go Back |
Conditions for large angle scatteringRegardless of the nature of the force in an elastic collision, to get a scattering angle greater than 90 degrees, the target must be more massive than the projectile. 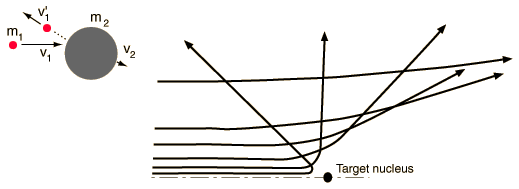 |
Index Rutherford concepts Scattering concepts Beiser reference | ||
|
Go Back |
Determining the Impact ParameterBesides the masses of the target and projectile, the scattering angle depends upon the force and upon the impact parameter. The impact parameter is the perpendicular distance to the closest approach if the projectile were undeflected. 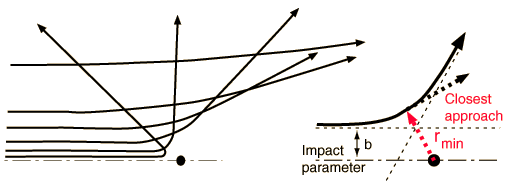
The default calculation above will be the calculation of the impact parameter b and the radius of closest approach. However, if you substitute a number for the radius of closest approach, it will calculate the kinetic energy necessary to produce that value, given the angle and other parameters.
|
Index Rutherford concepts Scattering concepts Beiser reference Fowles reference | ||||
|
Go Back |