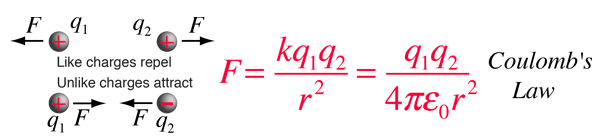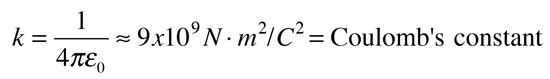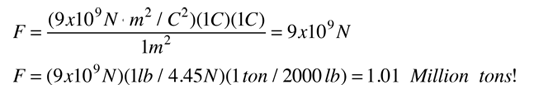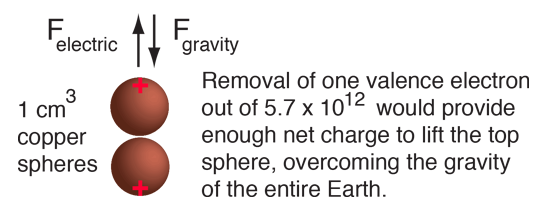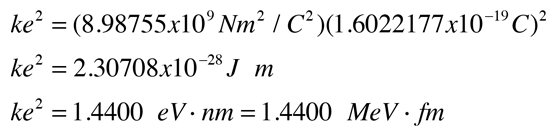Electric Force Example
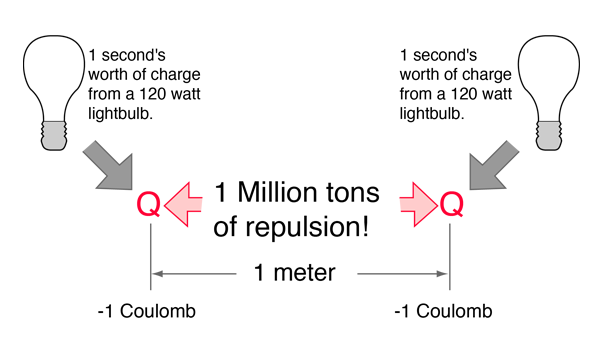
The electric force between charges may be calculated using Coulomb's law.
Normal household circuits in the U.S. operate on an AC voltage of about V =120 volts. Connected to such a ciruit, the electric power relationship P = IV tells us that to use power at the rate of P = 120 watts on a 120 volt circuit would require an electric current of I = 1 ampere. One ampere of current transports one Coulomb of charge per second through the conductor. So one Coulomb of charge represents the charge transported through a 120 watt lightbulb in one second.
If two one-second collections of 1 Coulomb each were concentrated at points one meter apart, the force between them could be calculated from Coulomb's Law. For this particular case, that calculation becomes
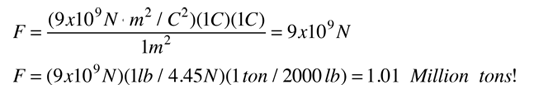
If two such charges could indeed be concentrated at two points a meter apart, they would move away from each other under the influence of this enormous force, even if they had to rip themselves out of solid steel to do so!
If such enormous forces would result from our hypothetical charge arrangement, then why don't we see more dramatic displays of electrical force? The general answer is that at a given point in a wire, there is never very much departure from electrical neutrality. Nature never collects a Coulomb of charge at one point. It might be instructive to examine the amount of charge in a sphere of copper of volume one cubic centimeter. Copper has one valence electron outside of closed shells in its atom, and that electron is fairly free to move about in solid copper material (that's what makes copper a good electrical conductor). The density of metallic copper is about 9 grams/cm3 and one mole of copper is 63.5 grams so the cubic centimeter of copper contains about 1/7th of a mole or about 8.5 x 1022 copper atoms. With one mobile electron per atom, and with the electron charge of 1.6 x 10-19 Coulombs, this means there are about 13,600 Coulombs of potentially mobile charge in one cm3 of copper. Suppose we remove enough of the electrons from two spheres of copper so that there is enough net positive charge on them to suspend one of them over the other. What fraction of the electron charge must we remove? The force to lift one of the spheres of copper would be its weight, 0.088 Newtons. Assuming that the net charge resides at the points of the spheres most distant from each other because of the charge repulsion, we can set the force of repulsion equal to the weight of a sphere. The radius of a one cm3 sphere is 0.62 cm, so we will treat the force as that between two point charges 2.48 cm apart (i.e., twice the sphere diameter apart). Using Coulomb's law, this requires a charge of 7.8 x 10-8 Coulombs. Compared to the total mobile charge of 13,600 Coulombs, this amounts to removing just one valence electron out of every 5.7 trillion (5.7 x 1012) from each copper sphere. The final result is that the removal of just one out of roughly six trillion of the free electrons from each copper sphere would cause enough electric repulsion on the top sphere to lift it, overcoming the gravitational pull of the entire Earth!
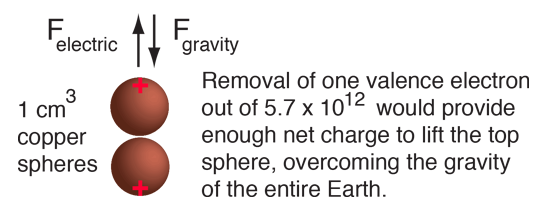
|
Index
Electromagnetic force |