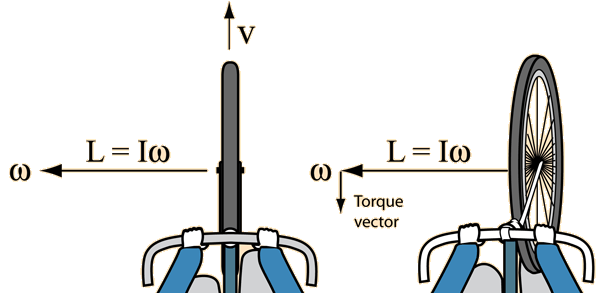
Bicycle Wheel
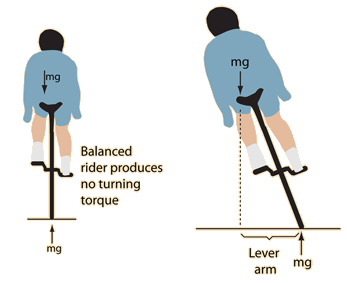
| The angulur momentum of the turning bicycle wheels makes them act like gyroscopes to help stabilize the bicycle. This gyroscopic action also helps to turn the bicycle. Having pointed to the gyroscopic nature of the bicycle wheel, it should be pointed out that experiments indicate that the gyroscopic stability arising from the wheels is not a significant part of the stability of a bicycle. The moments of inertia and the speeds are not large enough. The experiments and review of Lowell and McKell indicate that the stability of the bicycle can be described in terms of centrifugal force. A rider who feels an unbalance to the left will turn the handlebars left, producing a segment of a circular path with resulting centrifugal force which pushes the top of the bicycle back toward vertical and a balanced condition. Presumably the larger masses and speeds of motorcycle wheels do make the gyroscopic torques a much larger factor with motorcycles. |
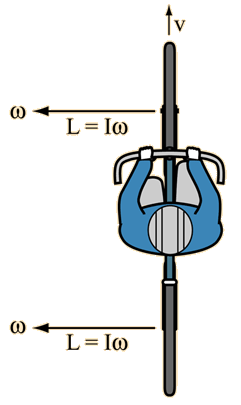 |
Vector rotation examples
Reference
Lowell and McKell
| HyperPhysics***** Mechanics *****Rotational motion | R Nave |