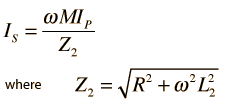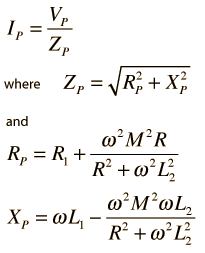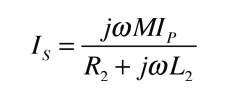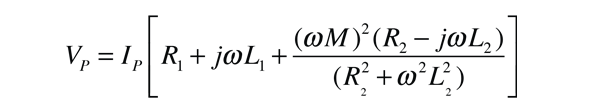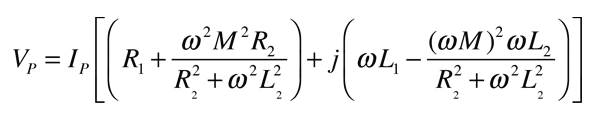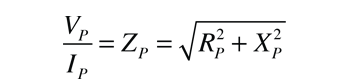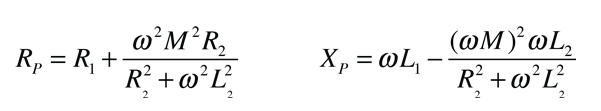Circuit Equations:Transformer
The application of the voltage law to both primary and secondary circuits of a transformer gives:
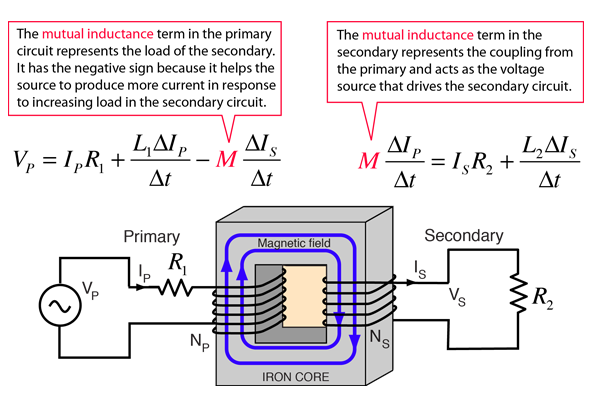
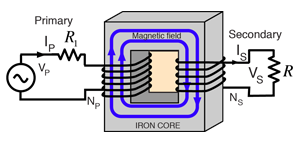
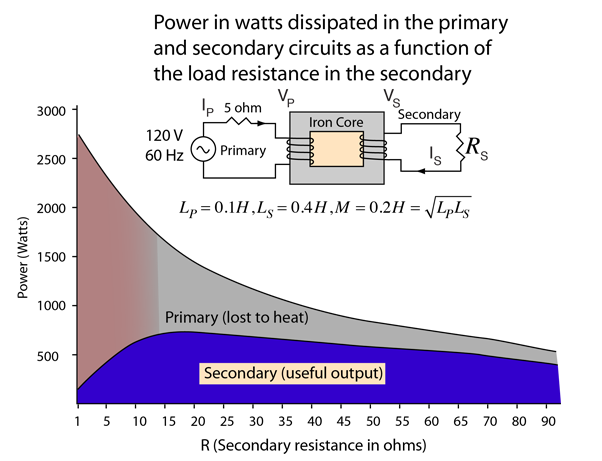
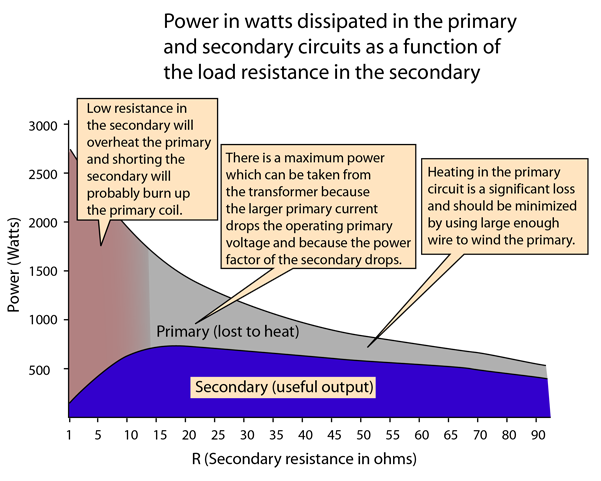
The transformer is the most common application of the concept of mutual inductance. In the transformer, the effect of the mutual inductance is to cause the primary ciruit to take more power from the electrical supply in response to an increased load on the secondary. For example, if the load resistance in the secondary is reduced, then the power required will increase, forcing the primary side of the transformer to draw more current to supply the additional need.
| Circuit Equation Solutions | Calculation |
Transformer concepts
Faraday's law concepts
Inductance concepts
| HyperPhysics***** Electricity and Magnetism | R Nave |