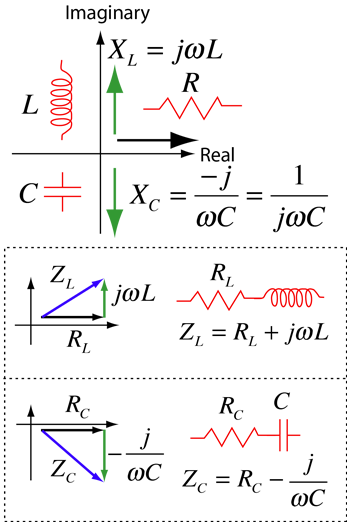
Use of Complex Impedance
The handling of the impedance of an AC circuit with multiple components quickly becomes unmanageable if sines and cosines are used to represent the voltages and currents. A mathematical construct which eases the difficulty is the use of complex exponential functions. The basic parts of the strategy are as follows:
|
| 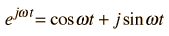
| Polar form of complex number | |
|
|  | ||
|
| 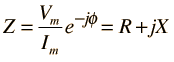 | Impedance combinations | Phasor diagrams |
|
| 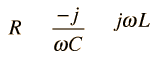 | RL and RC combinations | Example for parallel elements |
AC circuit concepts
| HyperPhysics***** Electricity and Magnetism | R Nave |