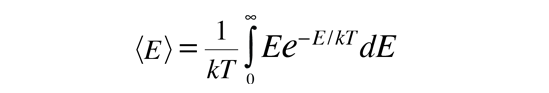Average Particle Energy from Boltzmann Distribution
The Boltzmann distribution describes the distribution of energy among classical (distinguishable) particles:
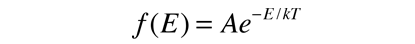
It can be used to evaluate the average energy per particle in the circumstance where there is no energy-dependent density of states to skew the distribution. To represent the probability for a given energy, it must be normalized to a probability of 1 :
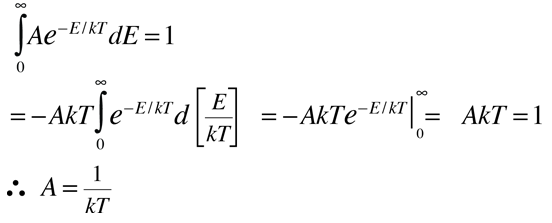
This normalized distribution function can then be used to evaluate the mean or average energy.
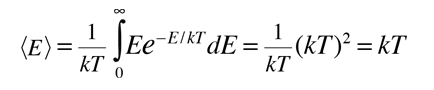 |
|
This shows that the average energy = kT when the energy is randomly distributed among the available energy states. The development of the Boltzmann distribution was under the constraints of conservation of energy and conservation of the number of particles. Note that this average energy for randomly distributed energy is not the same as the average kinetic energy.
| Applications of the Boltzmann distribution |
Kinetic theory concepts
| HyperPhysics***** Thermodynamics | R Nave |