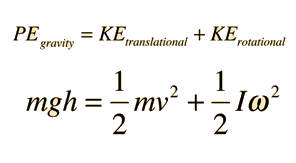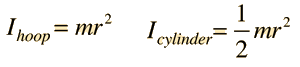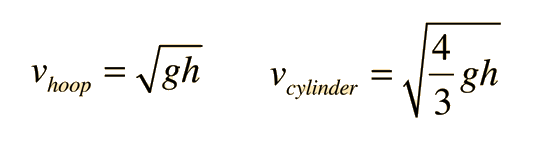Hoop and Cylinder Motion
Given a race between a thin hoop and a uniform cylinder down an incline. Which will win?
 |
Do the relative masses of the hoop and cylinder affect the outcome? Do the relative radii of the hoop and cylinder affect the outcome? Both start at the same height and have gravitational potential energy = mgh. Assume that they roll without slipping. |
The analysis uses angular velocity and rotational kinetic energy. For rolling without slipping, the linear velocity and angular velocity are strictly proportional.
Rotation concepts
Rotational kinetic energy concepts
| HyperPhysics***** Mechanics | R Nave |