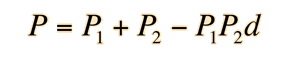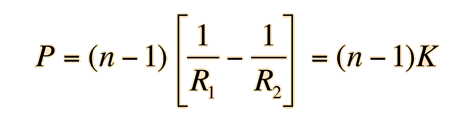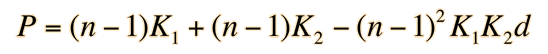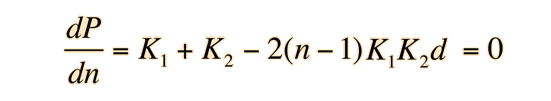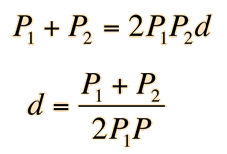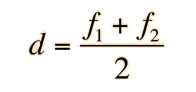Spaced Doublet Approach to Chromatic Aberration
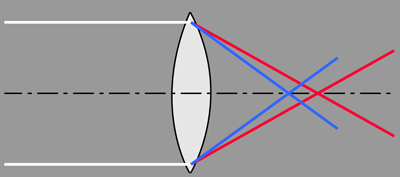
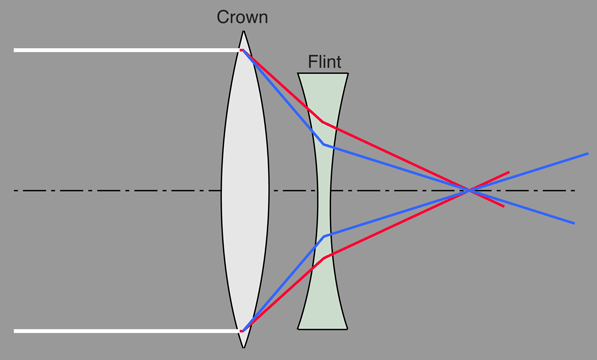
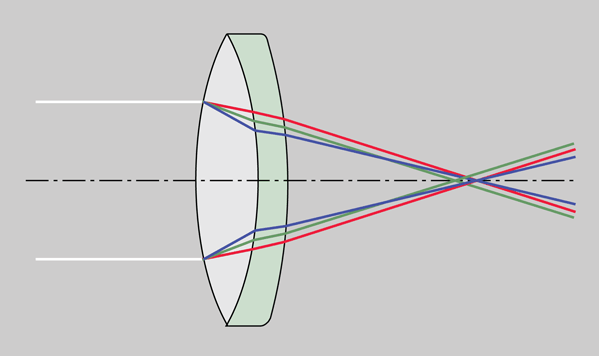
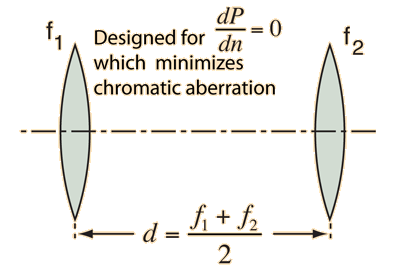 | Another approach to chromatic aberration reduction is to use two positive lenses separated by one half the sum of their wavelengths. Two equal positive lenses are used in eyepieces like the Ramsden eyepiece for correction. |
This approach to minimizing chromatic aberration uses two lenses of the same type of glass so that there is just one index of refraction n, and the expression for the combined power of the lens combination depends upon that index of refraction. If you take the derivative of the power expression with respect to n and set it equal to zero, you can solve for the required separation of the lenses which makes that derivative equal to zero. The variation of index of refraction with light wavelength or color is called dispersion, and the zero derivative implies that the dispersion is zero. If the power does not depend on the index of refraction n, you have eliminated chromatic aberration. The caveat is that these expressions presume thin lenses and paraxial rays (close to optical axis), so it is not a perfect solution.
The power of a pair of thin lenses is given by
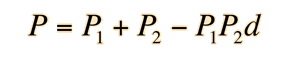
where the individual lens powers for a thin lens can be expressedd as
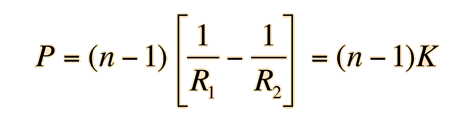
from the lens-makers formula. Here, K will be used to represent the dependence upon the radii of the lens surfaces. The power for the lens pair is then
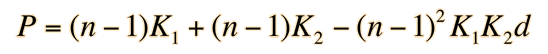
The derivative of the power with respect to n is
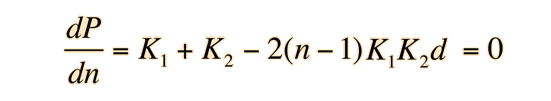
This is the condition for no change in lens power with respect to the index n, i.e., zero chromatic aberration. Multiplying by (n-1) allows us to express this in terms of the lens powers and yields
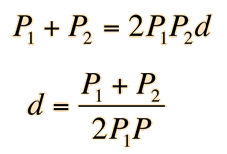
And using P=1/f this can be expressed in terms of the focal lengths
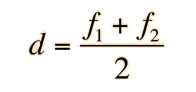
Note that if f1 = f2 the separation is just equal to the focal length of each of the lenses, and this condition is used for the Ramsden eypiece as mentioned above.
|