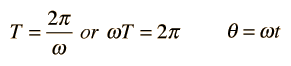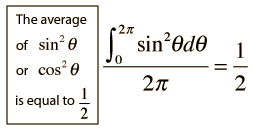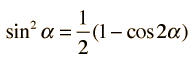Instantaneous Power
As in DC circuits, the instantaneous electric power in an AC circuit is given by P=VI where V and I are the instantaneous voltage and current.
Since
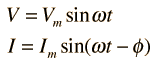 then the instantaneous power at any time t can be expressed as |
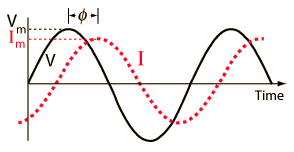 |
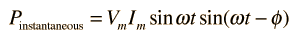
and using the trig identity
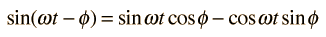
the power becomes:
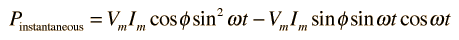
Averaging this power over a complete cycle gives the average power.
AC Circuits
| HyperPhysics*****Electricity and magnetism | R Nave |
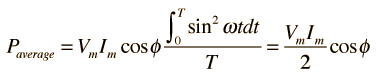
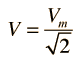
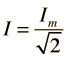 ,
,