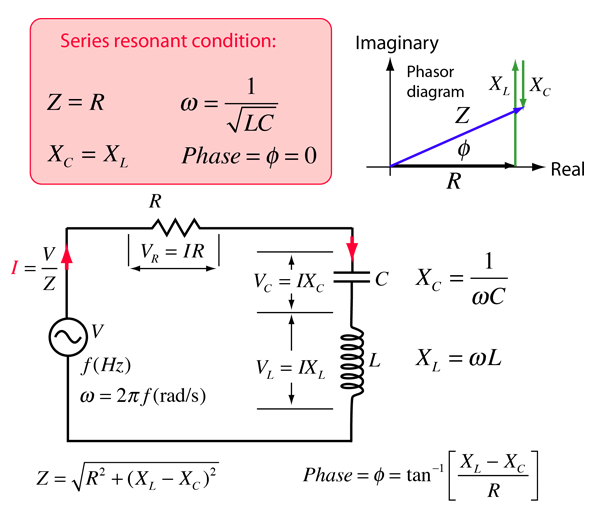
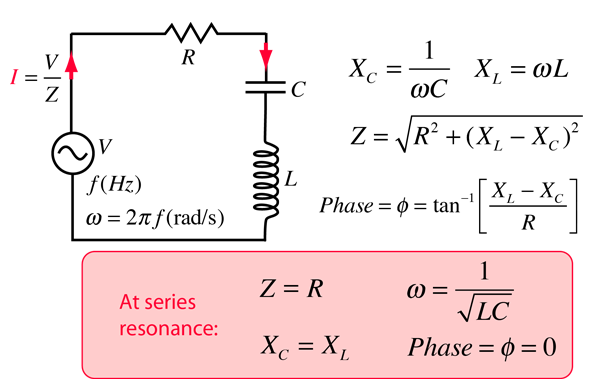
RLC Series Impedance
The frequency dependent impedance of an RLC series circuit
When exploring the values for real circuits, it is easy to find examples where both VL and VC are larger than the resultant voltage V. This can occur because these voltages VL and VC act 180° out of phase with each other. You can visualize this from the phasor diagram by seeing that both VL and VC can be large and that they exactly cancel each other at resonance.
Default values will be entered for unspecified parameters, but all component values can be changed. Click outside the box after entering data to initiate the calculation.
|
Index
Capacitance concepts
Inductance concepts
AC circuit concepts

Resonant Frequency Calculator |