AC Ohm's Law
The AC analog to Ohm's law is
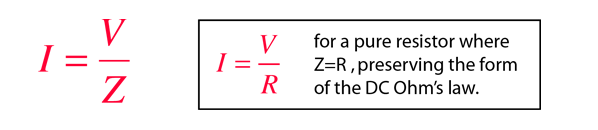
where Z is the impedance of the circuit and V and I are the rms or effective values of the voltage and current. Associated with the impedance Z is a phase angle, so that even though Z is also the ratio of the voltage and current peaks, the peaks of voltage and current do not occur at the same time. The phase angle is necessary to characterize the circuit and allow the calculation of the average power used by the circuit.
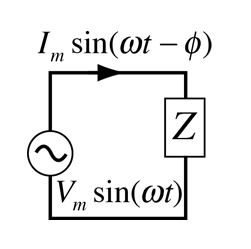 |
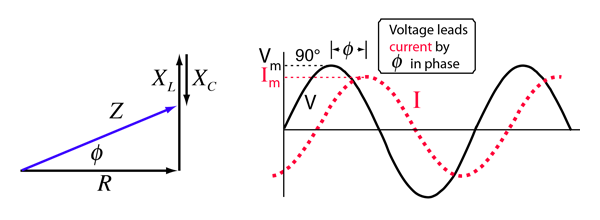
The illustration is for a case where the inductive reactance is dominant over the capacitive reactance as shown in the phasor diagram.
Default values will be entered for V and Z above if they are left unspecified, but those values can be changed. If the current is changed, then Z will be recalculated. If a phase angle outside the allowed range -90 to +90 is entered, it will be replaced by a default value.
Note: The above treatment of Ohm's law is valid for typical wires and elements used for household electricity which is at 60Hz frequency. For these low frequencies, the current density in wires can be assumed to be constant across the cross-section of a wire. This is not true for high frequencies like radio frequencies and above. For such frequencies the magnetic effects are significant and the currents are predominantly in the outer parts of the conductors. This is typically called the "skin effect", and must be taken into account in the design of high frequency circuits.
AC circuit concepts
| HyperPhysics***** Electricity and Magnetism | R Nave |