Reflection and Transmission of Plane Waves
When a plane pressure wave strikes a plane surface between two media, part of the wave will be transmitted and part reflected. The amount reflected and transmitted is generally characterized by a quantity called the acoustic impedance, which for a uniform medium is equal to the density times the wave speed, z = ρv, where ρ is the density and v is the velocity of sound in the medium.
The example of a wave traveling from the left to strike an interface between two media will be used. The pressure for the incident, reflected and transmitted waves for a given frequency may be expressed as:
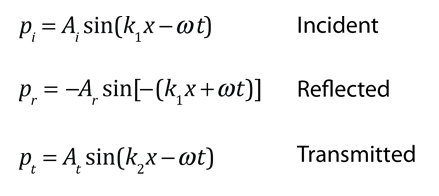
These are of the same form as the solution to the wave equation for a string wave except that the variable that is varying sinusoidally is the pressure. For sound waves traveling in a solid, the sound speed is expressed in terms of the bulk modulus B, a measure of the elastic property of the solid. The quantity k =2π/λ , λ = wavelength, and ω = 2πf.
The pressure boundary condition at the interface between two media, pi + pr = pt, leads by substitution to the expressions for the reflection coefficient Rp and transmission coefficient Rt:
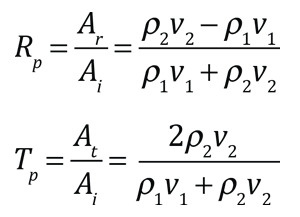
The following example is taken from the article referenced below on the reflection and transmission of ultrasonic waves. It involves a pressure wave traveling across a plane boundary between steel and water.
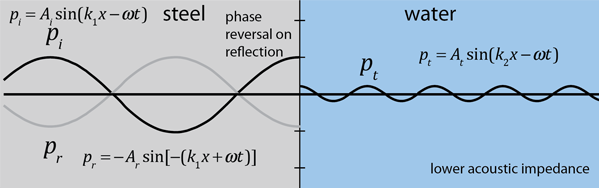
The acoustic impedances ρv of steel and water are given as:
Steel: ρsvs = 46.5 x 106 kg/m2s
Water: ρwvw = 1.5 x 106 kg/m2s
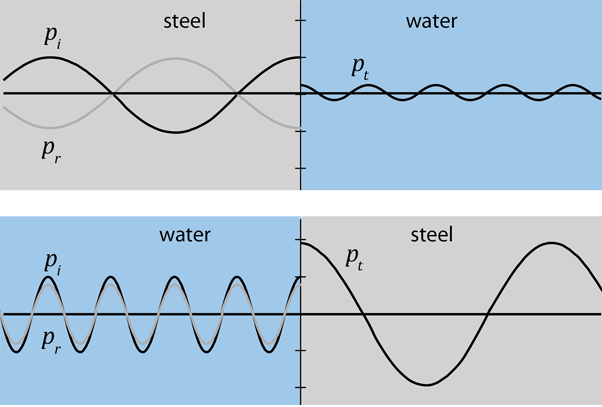
For a pressure wave traveling from steel to water, this leads to the coefficients: Reflection: Rp = -9.38, Transmission Tp = 0.063
Note that the reflection from the boundary with a medium of lower acoustic impedance leads to a phase reversal of the wave and a small amount of transmission into the lower impedance medium.
For a pressure wave traveling from water to steel, the coefficients are:
Reflection: Rp = 9.38, Transmission Tp = 1.938
The reflection from the steel medium with its higher acoustic impedance does not involve a phase change, and leads to a larger amplitude and larger wavelength in the steel. The steel is characterized by a higher propagation speed and longer wavelength.
Reference: http://www.fast.u-psud.fr/~martin/acoustique/support/rˇflection-rˇfraction.pdf
| HyperPhysics***** Sound | R Nave |