Bulk Elastic Properties
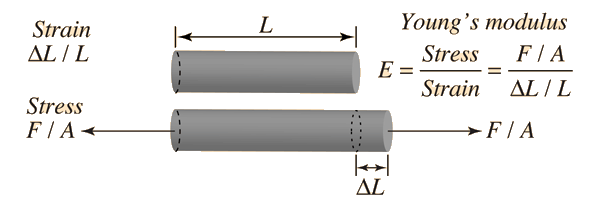
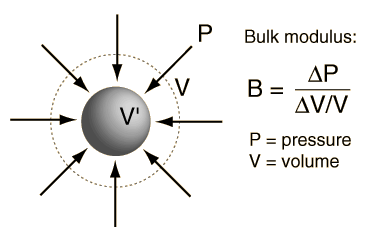
The bulk elastic properties of a material determine how much it will compress under a given amount of external pressure. The ratio of the change in pressure to the fractional volume compression is called the bulk modulus of the material.
|
A representative value for the bulk modulus for steel is 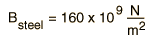 and that for water is 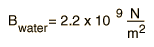 The reciprocal of the bulk modulus is called the compressibility of the substance. The amount of compression of solids and liquids is seen to be very small. |
 |
The bulk modulus of a solid influences the speed of sound and other mechanical waves in the material. It also is a factor in the amount of energy stored in solid material in the Earth's crust. This buildup of elastic energy can be released violently in an earthquake, so knowing bulk moduli for the Earth's crust materials is an important part of the study of earthquakes. The bulk modulus is a factor in the speed of seismic waves from earthquakes.
A common statement is that water is an incompressible fluid. This is not strictly true, as indicated by its finite bulk modulus, but the amount of compression is very small. At the bottom of the Pacific Ocean at a depth of about 4000 meters, the pressure is about 4 x 107 N/m2. Even under this enormous pressure, the fractional volume compression is only about 1.8% and that for steel would be only about 0.025%. So it is fair to say that water is nearly incompressible. Reference: Halliday, Resnick, Walker, 5th Ed. Extended.
John Hermance points out that for a more accurate picture of the compressibility of water, the temperature should be taken into account. The reason the 1.8% compression can be quoted above is that the compressibility of the water at 20°C at the surface is about the same as the compressibility at 4000m depth if the temperature at the bottom is 5°C. The compressibility at that pressure and depth has a higher value because of the colder temperature than it would have had at 20°C. Using the detailed compressibility data for water from the Fine & Millero compilation, it can be seen that if the bottom temperature were 5°C the compression would be about 1.82%, but if it were 20°C the amount of compression would be about 1.66%.
°C | Atm | per Mbar | at 400 bars |
Another way to state it is that if the bottom temperature is 5°C the compressibility would decrease by only 0.9% from surface to depth, whereas if the bottom temperature were also 20°C, the compressibility would decrease by about 9.6%.
Hermance's interest in this detailed compressibility picture comes from the application to the compressibility of groundwater in the Earth's subsurface. This groundwater could be at a higher temperature, and the change in compressibility is of considerable importance in the understanding of the storage and release of groundwater from cracks and pores in the rock, as well as the effects of hydrofracturing, earthquakes, etc., in the Earth's upper crust.
| Compressibility of Liquids |
Reference: Fine, R. A. and Millero, F. J., 1973. "Compressibility of water as a function of temperature and pressure", Journal of Chemical Physics 59(10):5529-5536. doi: 10.1063/1.1679903.
Periodic motion concepts
| HyperPhysics***** Mechanics | R Nave |